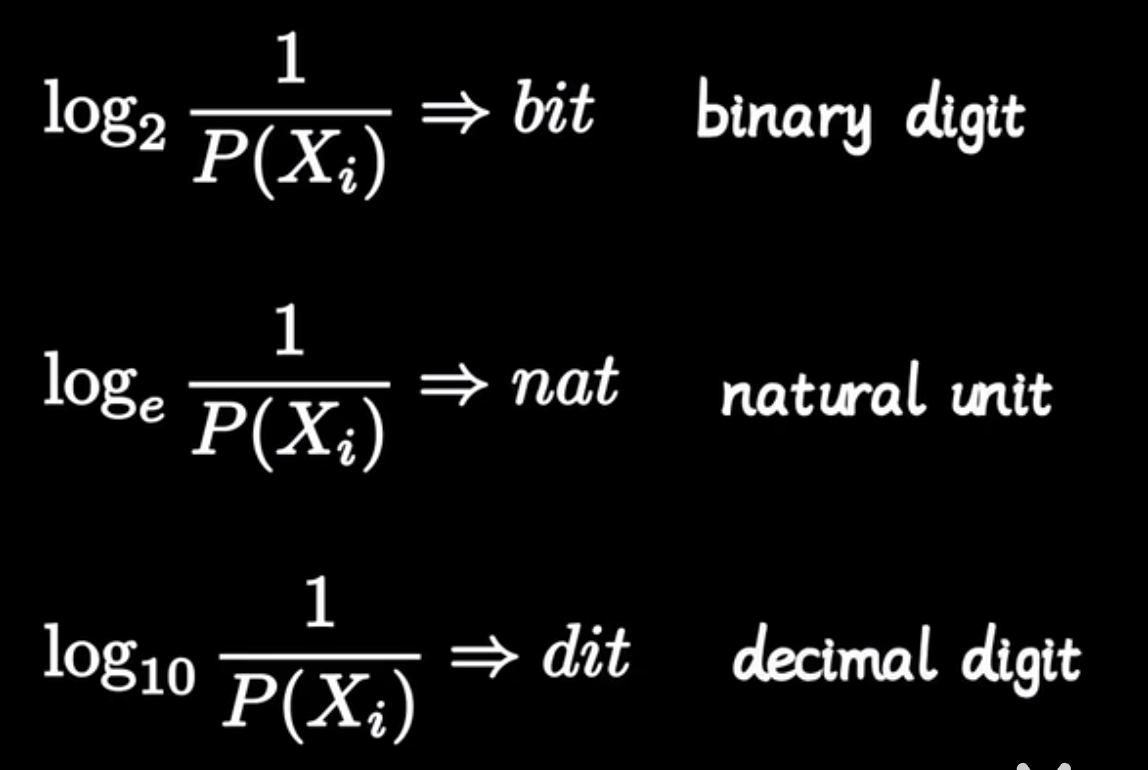信息熵

在信息论中，熵(entropy)用于表示是接收的每条消息中包含的信息的平均量，也可以理解成随机变量的不确定性（这里的想法是，比较不可能发生的事情，当它发生了，会提供更多的信息）¹

特性

设X是一个有限状态的离散型随机变量，其概率分布为

$$P(X=x_i)=p_i,i=1,2,\dots ,n$$

那么随机变量X的熵定义为

$$H(X)=-\sum _{i=1}^n(p_i\log p_i)$$

熵越大，那么随机变量的不确定性就越大

公式理解

改写一下：将负号移到对数里面

$$H(X)=\sum _{i=1}^n{p}_i\log \frac{1}{p_i}$$

现在$\frac{1}{p_i}$表示不确定性

取$\log \frac{1}{p_i}$表示这个不确定性需要的比特数字，也就是复杂程度。不同的底数表示不同的编码方式。

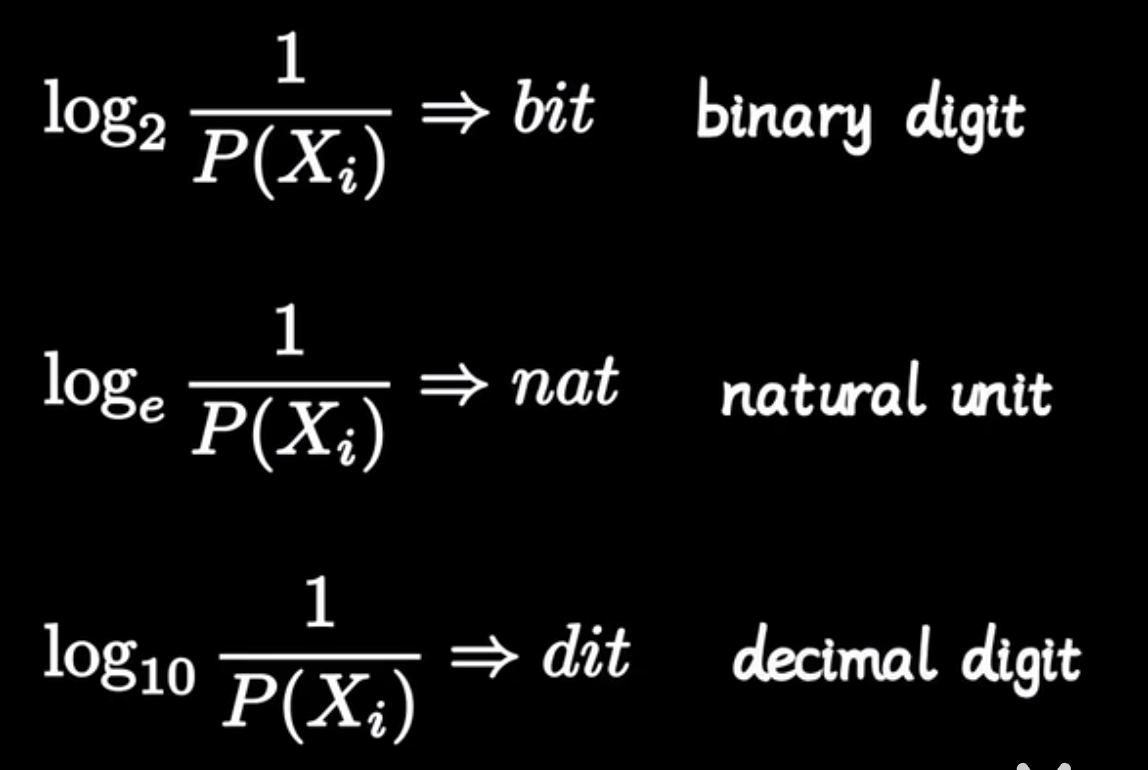
现在乘上$p_i$表示加权，那么熵公式表示的是表示概率的平均复杂程度。

AI中各种熵的相互关系

信息熵

$$H(X)=-\sum _i^{n}p(x_i)\log p(x_i)$$

联合熵

$$H(X,Y)=-\sum _x\sum _{y}p(x,y)\log p(x,y)$$

条件熵

$$\overline{H}(Y|X)=-\sum _x\sum _{y}p(x,y)\log p(y|x)$$

互信息（信息增益）

$$\begin{array}{r}I(X,Y)=\sum _{x,y}p(x,y)\text{log}\frac{p(x,y)}{p(x)p(y)}\end{array}$$

交叉熵

$$L(p,q)=-\sum _{i}p(x_i)\log q(x_i)$$

相对熵（KL离散度）

$$D_{KL}(p\Vert q)=\sum _{i}p(x_i)\log \frac{p(x_i)}{q(x_i)}$$

Reference

Footnotes

1. 熵 (信息论) - 维基百科，自由的百科全书 ↩