4-决策树

[TOC]

简介

• 本质：从训练数据中归纳出一组分类规则，与训练数据集不矛盾
• 假设空间：无穷多个条件概率模型
• 策略：最小化损失函数
• 特征选择：递归地选择最优特征
• 生成：对应特征空间的划分，直到所有的训练子集都被基本正确的划分
• 剪枝：避免过拟合，提高泛化能力

4.1-基本流程

决策树(DTs)是一种用于分类和回归的非参数有监督学习方法。

其目标是创建一个模型，通过学习从数据特性中推断出的简单决策规则来预测目标变量的值¹。

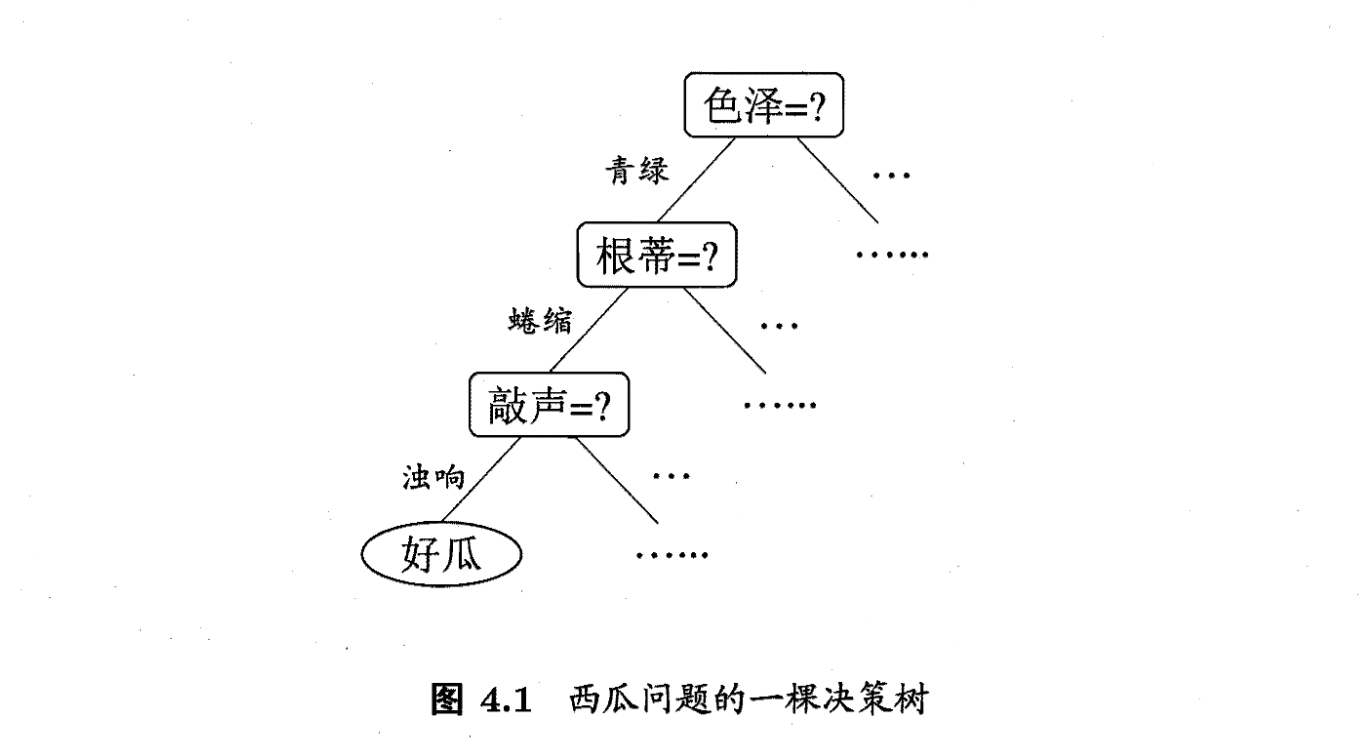
例如，在西瓜例子中，我们可以先观察西瓜颜色，然后在此条件下再次决策（子决策），直到能够判断出好瓜还是坏瓜。

这里给出决策树学习基本算法的伪代码

sklearn中的决策树api演示：

from sklearn.datasets import load_iris
from sklearn import tree
X, y = load_iris(return_X_y=True)
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X, y)
tree.plot_tree(clf)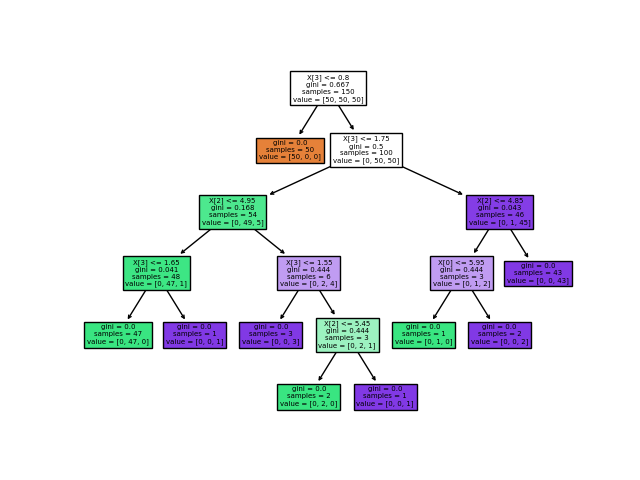 

4.2-划分

当我们的属性变得比较多，那么决策树就会变得很长，这时候需要的是一个高效的决策树，使得我们能够以尽量小的决策步骤将数据划分出来，或者说一次划分尽可能多的数据。

4.2.1-信息增益(ID3)

在信息论中，熵可以衡量随机变量的不确定性，上越大就表明信息越不明确。

信息的整体的熵：

$$\mathrm{Ent}(D)=-\sum _{k=1}^{|\mathcal{Y}|}{p}_k{\log }_2{p}_k\text{\hspace{1em}(4.1)}$$

假定离散属性 $a$ 有 $V$ 个取值，那么可以计算 $a$ 取值为 $v$ 时的熵² $D^v$, 考虑到样本数量的影响，最终得到信息增益

$$\mathrm{Gain}(D,a)=\mathrm{Ent}(D)-\sum _{v=1}^V\frac{\left|D^v\right|}{|D|}\mathrm{Ent}\left(D^v\right)\text{\hspace{1em}(4.2)}$$

那么只需要递归地选取能使信息增益最大化的属性 $a_{\ast }$ 就行，即$a_{\ast }=\underset{a\in A}{\mathrm{argmax}}\mathrm{Gain}(D,a)$。这就是ID3算法

4.2.2-信息增益率(C.45)

C4.5决策树的提出完全是为了解决ID3决策树的一个缺点，当一个属性的可取值数目较多时，那么可能在这个属性对应的可取值下的样本只有一个或者是很少个，那么这个时候它的信息增益是非常高的，这个时候纯度很高，ID3决策树会认为这个属性很适合划分，但是较多取值的属性来进行划分带来的问题是它的泛化能力比较弱，不能够对新样本进行有效的预测。³

与ID3算法不同，C4.5算法使用信息增益率来划分决策树

$$Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}\text{\hspace{1em}(4.3)}$$

其中

$$IV(a)=\sum _{v=1}^V\frac{|D^v|}{D}{\log }_2\frac{|D^v|}{|D|}\text{\hspace{1em}(4.4)}$$

但是增益率准则对可取值数目较少的属性有所偏好，于是C4.5会先算信息增益，找到大于平均值的然后选取其中增益率最高的划分。

4.2.3-基尼指数(CART)

CART决策树使用基尼指数划分

基尼值表示任意取两个样本，其不一致的概率：

$$Gini(D)=\sum _{k=1}^{|y|}\sum _{k^{\prime }\ne k}{p}_k{p}_{k^{\prime }}=1-\sum _{k=1}^{|y|}{p}_k^2\text{\hspace{1em}(4.5)}$$

基尼指数：

$$Gini\_index(D,a)=\sum _{v=1}^V\frac{|D^v|}{D}Gini(D^v)$$

4.3-剪枝处理

剪枝处理是避免模型过拟合的常用手段，常见的有预剪枝和后剪枝。 预剪枝：决策树生成过程中，在划分前估计，如果不能提升泛化能力，那么停止 后剪枝：决策树生成后，自底向上，将不能提示泛化能力的叶子节点剪掉

4.4-连续与缺失值

4.4.2-连续值处理

当属性的取值不再离散时，我们需要做什么？连续值离散化 最简单的策略：二分法(bi-partition)，对于数学 $a$ 的取值，按照数值划分成大于和小于的两种，这里取排序后相邻取值的中位数作为划分边界。

$$T_a=\left\{\frac{a_i+a_{i+1}}{2}|1\le i\le n-1\right\}\text{\hspace{1em}(4.7)}$$ $$\begin{array}{rl}\mathrm{Gain}(D,a)& =\underset{t\in T_a}{\max }\mathrm{Gain}(D,a,t)\\ & =\underset{t\in T_a}{\max }\mathrm{Ent}(D)-\sum _{\lambda \in \{-,+\}}\frac{\left|D_t^{\lambda }\right|}{|D|}\mathrm{Ent}\left(D_t^{\lambda }\right)\end{array}\text{\hspace{1em}(4.8)}$$

4.4.1-缺失值处理

数据中常有缺失值，如果直接丢弃，那么数据集的浪费将是指数级的。

这时我们面临两个问题： (1) 如何在属性值缺失的情况进行划分属性选择？

1. 去掉该属性缺失的属性值对应的样本
2. 计算信息增益
3. 用无缺失值的样本所占比例乘以去除缺失值的属性的信息增益

$$\begin{array}{rl}\mathrm{Gain}(D,a)& =\rho \times \mathrm{Gain}(\tilde{D},a)\\ & =\rho \times \left(\mathrm{Ent}(\tilde{D})-\sum _{v=1}^V{\tilde{r}}_v\mathrm{Ent}\left({\tilde{D}}^v\right)\right)\end{array}\text{\hspace{1em}(4.12)}$$

(2) 给定划分属性，若样本在该属性上的值缺失，如何对样本进行划分？

1. 将该样本放到所有的分支中，并赋以不同的权重，权重为各分支的样本数占排除该属性值为缺失的样本总数比例。
2. 相当于让同一个样本以不同的概率划入到不同的子结点中去.

4.5-多变量决策树

假设你在西瓜数据集上训练出了一下决策树 其分类边界如下图所示

仔细观察会发现有几道弯，是否有办法简化一下决策树呢？ 其实可以组合 含糖率 与 密度，构造一个新属性

以上图为例，其构造了两个新属性：

• -0.8密度 - 0.044含糖率 <= -0.313
• -0.365密度 + 0.366含糖率 <= -0.158

Footnotes

1. 1.10 决策树-scikit-learn中文社区 ↩

2. 这里不严谨，a的取值为 $\{a,a^1,a^2,\dots ,a^V\}$ ↩

3. ID3、C4.5、CART三种决策树的区别_夏末的初雪的博客-CSDN博客 ↩