模拟退火是一种随机化算法。当一个问题的方案数量极大(甚至是无穷的)而且不是一个单峰函数时,我们常使用模拟退火求解。
步骤
hill_climbing容易陷入局部最优,因此我们需要去接受这个非最优解从而跳出这个局部最优解,即为模拟退火算法。
如果新状态的解更优则修改答案,否则以一定概率接受新状态。 我们定义当前温度为 ,新状态 与已知状态 (新状态由已知状态通过随机的方式得到)之间的能量(值)差为 (),则发生状态转移(修改最优解)的概率为
\end{cases}$$
摘自OI-wiki
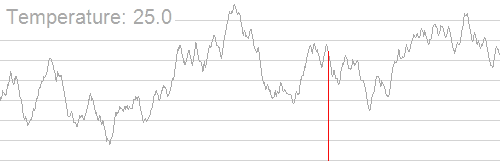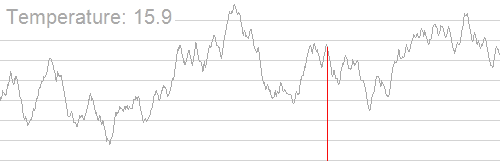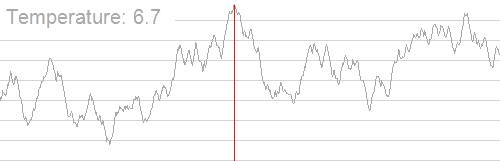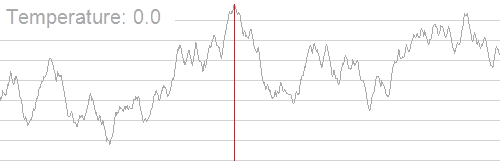
特点
- 全局搜索: 通过以一定概率接受”差解”,模拟退火算法能够跳出局部最优,在解空间中进行全局搜索。
- 收敛性: 随着温度的逐渐降低,算法接受”差解”的概率也逐渐降低,最终算法会收敛到一个近似最优解。
- 通用性: 模拟退火算法对问题的要求非常宽松,适用于各种离散和连续优化问题。
优化
- 分块:有时函数的峰很多,模拟退火难以跑出最优解。此时可以把整个值域分成几段,每段跑一遍模拟退火,然后再取最优解。