基本步骤
- 选择一个初始解作为当前解。
- 在当前解的邻域内寻找一个比当前解更优的解。
- 如果找到了更优解,则将其作为新的当前解,返回步骤2;否则,算法终止,当前解即为所得的局部最优解。
爬山算法(Hill Climbing)是一种启发式搜索算法,常用于解决优化问题。它的基本思想是:从一个初始解出发,不断寻找其”邻域”内的更优解,直到达到一个局部最优解。这个过程就像是在不断”爬山”,因此得名。
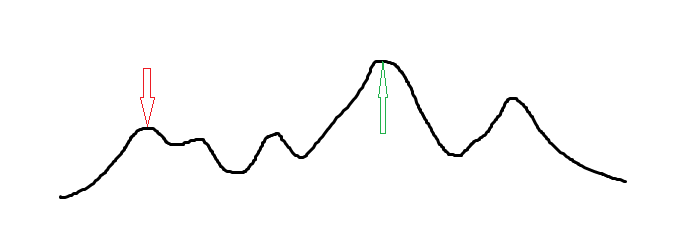
特点
- 局部搜索: 爬山算法每次只在当前解的邻域内寻找更优解,因此容易陷入局部最优。
- 贪心策略: 爬山算法总是选择邻域内最优的解作为下一步,因此是一种贪心算法。
- 简单高效: 爬山算法实现简单,通常能够快速找到一个较好的局部最优解。
- 容易陷入局部最优: 由于爬山算法只考虑当前解的邻域,因此无法跳出局部最优。这可能导致得到的解远远不如全局最优解。
- 解的质量依赖初始解: 不同的初始解可能会收敛到不同的局部最优解。因此初始解的选择对算法性能有很大影响。
改进
为了克服爬山算法的局限性,研究者提出了许多改进方法,如:
- 随机重启: 当算法收敛到一个局部最优解时,随机生成一个新的初始解重新开始搜索。多次重复这个过程,取所得局部最优解中的最优值。
- simulated_annealing: 允许算法以一定概率接受比当前解差的解,并随时间推移逐渐减小这个概率。这有助于算法跳出局部最优。
- 禁忌搜索: 记录最近访问过的一些解,在选择下一个解时避免重复访问这些解。
尽管有这些改进,爬山算法仍然难以稳定地求解大规模的NP-hard问题。但由于其简单高效的特点,爬山算法仍然在许多实际问题中得到了广泛应用,尤其是作为其他更复杂算法的初始化方法。