[TOC]
5.1-神经元模型
生物学上的神经元是指一个接受刺激,当刺激超过阈值后便会兴奋,并向后面的神经元发送信号。
这里是神经元指一个接受输入 ,并根据权重 计算总输入值,当兴奋程度超过阈值 便会根据**激活函数**输出 。
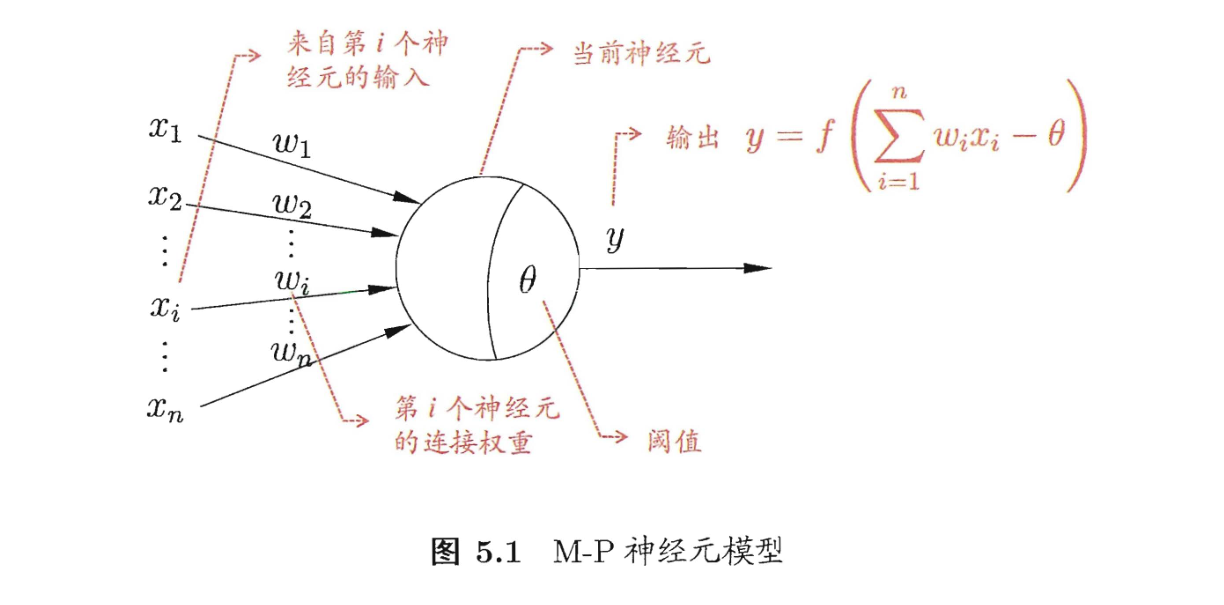
这里给出两个典型的激活函数,还记得线性模型里的单位跃迁函数和对数几率函数吗?这里可以把神经元看作一个线性模型

5.2-感知机与多层网络
感知机由两层神经元组成, 输入层接收外界输入信号后传递给输出层, 输出层是一个 M-P 神经元。
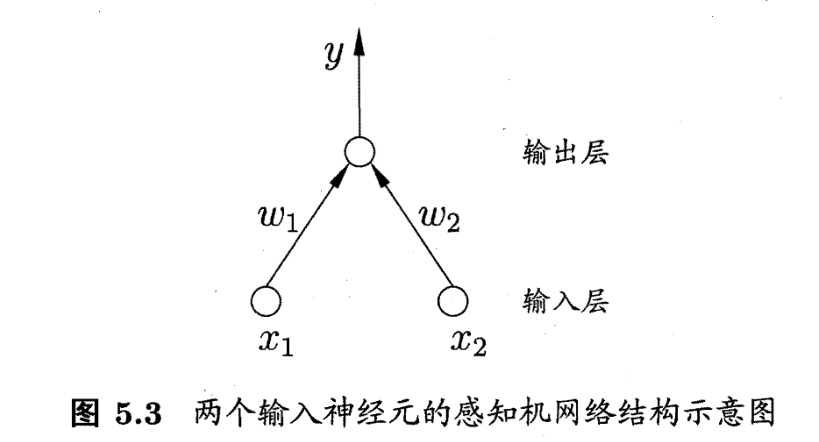
感应机只有输出层神经元进行激活函数处理,只有一层功能神经元,学习能力有限。
逻辑运算是线性可分问题,如果俩类是线性可分的,那么存在一个线性超平面将他们分开,感知机可以通过修改权重和阈值学习到(这里我当成线性模型中的学习)。反之不能,此时学习过程中会发送振荡,比如感知机就不能解决异或问题

不过虽然我们无法使用一个感知机解决异或问题,但是我们可以上升维度,随着维度升高,原本线性不可分的样本可能就会变成线性可分[^2]
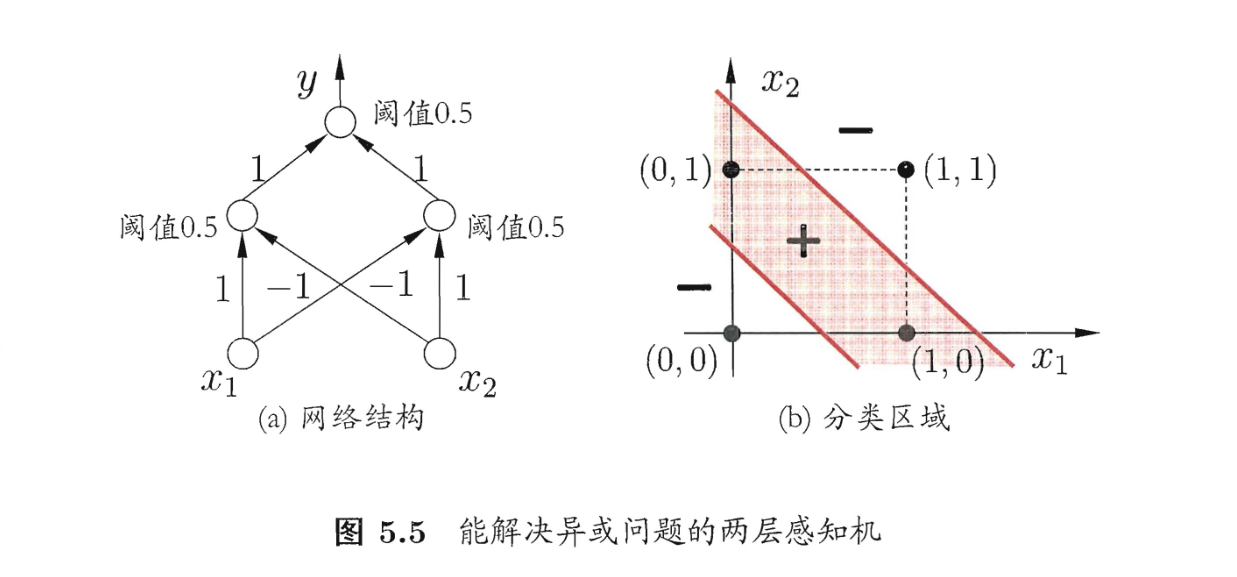
上图是一个能解决异或问题的二层感知机,这个感知机通过中间层的计算,对样本进行了升维操作,于是原本在二维下线性不可分的问题在三维空间下线性可分了

5.3-误差逆向传播
多层网络的学习能力比单层网络强得多,但是可能的权重和阈值的组合数也变多了,这时候需要更加强大的学习算法。
逆误差传播算法(Error Back Propagation),好像也叫反向传播,简称BP算法,算法形式如下
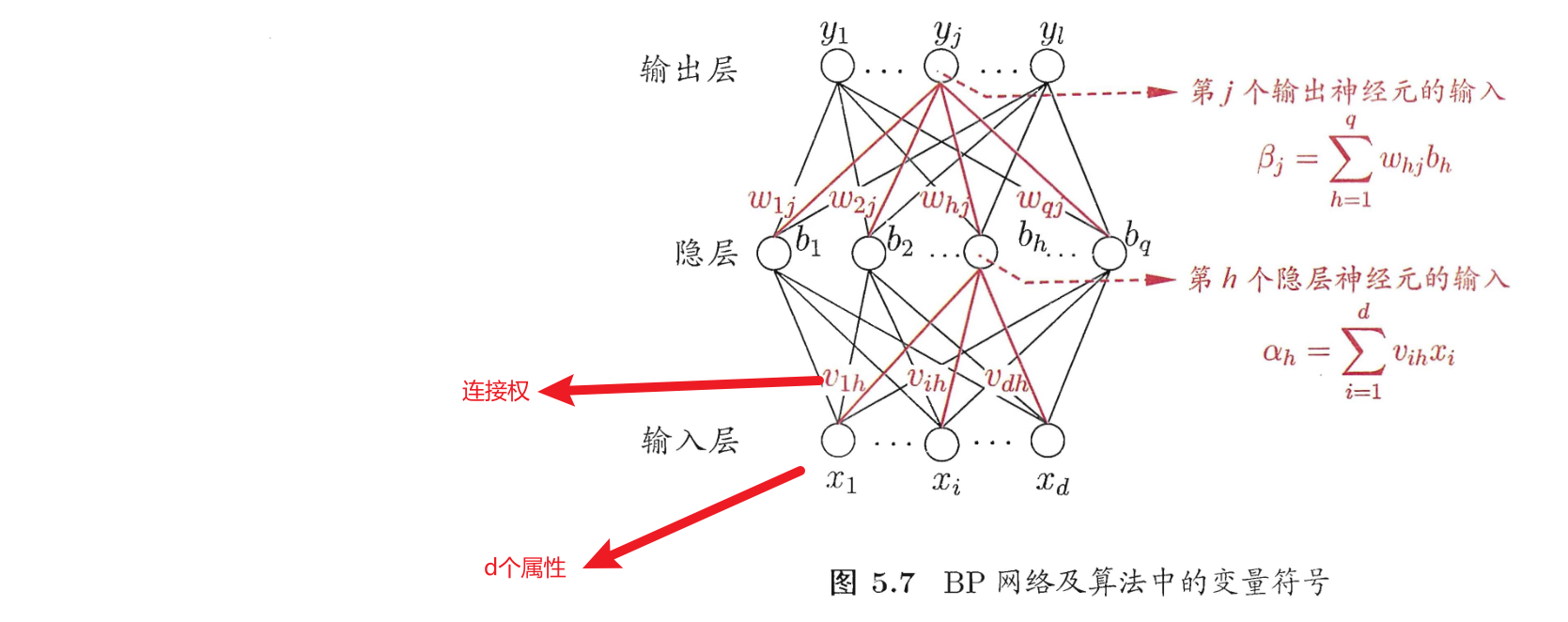
在训练时,假定有输入 ,输出 ,计算其均方误差
那么为了最小化均方误差,BP采用了梯度下降的方法,不断迭代地以目标的负梯度方向对参数进行调整:
给定学习率 和 均方误差,对于每一次迭代
其中
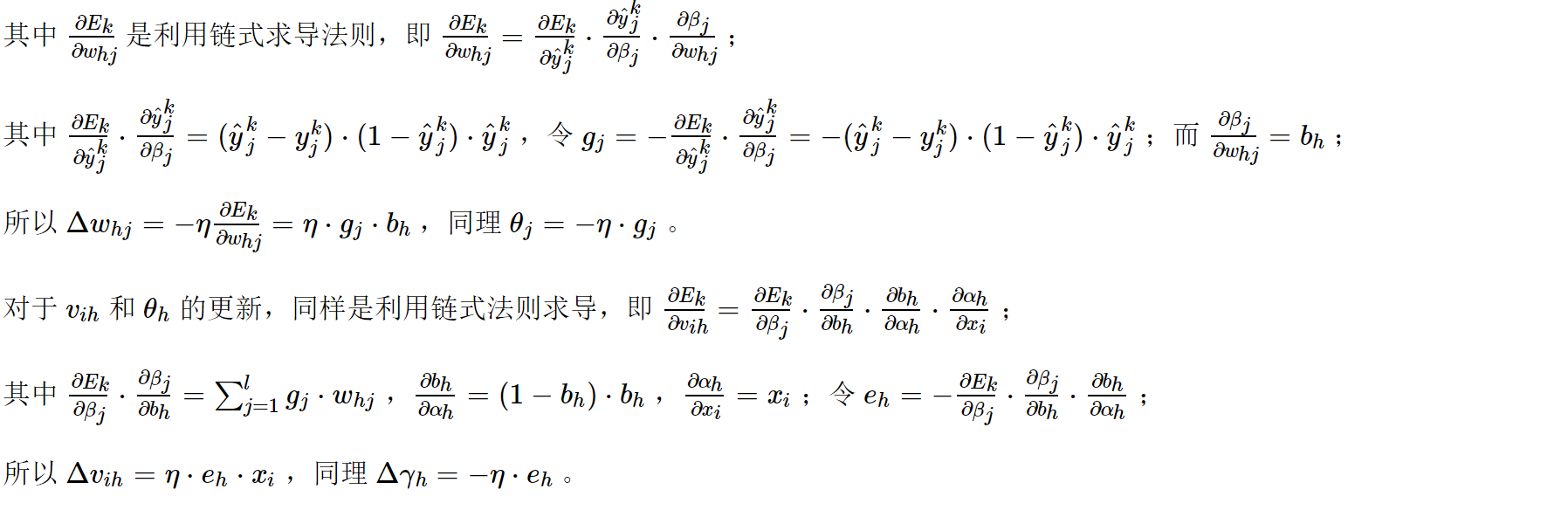
5.4-全局/局部最小
局部最小并不一定是全局最小,可能我们的算法在梯度下降时陷在局部最小出不去,得到的结果就不是最优的。 那么对于解决局部最小,业界有多种不同的方法:
- 开始时先让其搜索地广一点
- 模拟退火:每次有一定概率接受新的解
- 训练时不断变化学习率,自动调整
- 训练多个模型
- 训练多个神经网络,然后取效果最好的
- 训练后突然增大学习率,让其跳出最值点
- 随机梯度下降:在训练时会给梯度添加随机值,那么即使到了最值点,梯度也不是0
5.5-其他常见神经网络
5.6-深度学习
参考
- 机器学习笔记-神经网络(西瓜书第5章) | Travis (xucaixu.com)
- 《机器学习》西瓜书,周志华