高数公式整理

公式整理

[TOC]

泰勒

\begin{eqnarray} \sin x & = & x-\frac{x^{3}}{6}+o\left(x^{3}\right) \\ \arcsin x & = & x+\frac{x^{3}}{6}+o\left(x^{3}\right) \\ \cos x & = & 1-\frac{x^{2}}{2}+\frac{x^{4}}{24}+o\left(x^{4}\right) \\ \tan x & = & x+\frac{x^{3}}{3}+o\left(x^{3}\right) \\ \arctan x & = & x-\frac{x^{3}}{3}+o\left(x^{3}\right) \\ e^{x} & = & 1+x+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+o\left(x^{3}\right) \\ \ln (1+x) & = & x-\frac{x^{2}}{2}+\frac{x^{3}}{3}+o\left(x^{3}\right) \\ (1+x)^{\alpha} &=& 1+\alpha x+\frac{\alpha(\alpha-1)}{2} x^{2}+o\left(x^{2}\right) \\ \sqrt{1+x} &=& 1+\frac{1}{2}x - \frac{1}{8}x^2 + o(x^2) \\ \sqrt[3]{1+x} &=& 1+\frac{1}{3}x - \frac{1}{9}x^2 + o(x^2) \\ (1+x)^{\frac{1}{x}} &=& e-\frac{e}{2} x+\frac{11 e}{24} x^{2}-\frac{7 e}{16} x^{3}+o\left(x^{3}\right) \end{eqnarray}

习题常见

$$\begin{array}{rl}x-\ln (1+x)& \sim \frac{x^2}{2}\\ e^x-1-x& \sim \frac{x^2}{2}\\ 1-{\cos }^{a}x& \sim \frac{a{x}^2}{2}\\ f(x{)}^{g(x)}-1& \sim g(x)[f(x)-1]\left(f(x)\to 1\&\&f(x{)}^{g(x)}\to 1\right)\end{array}$$

微分

导数

$$\begin{array}{l}{\left(x^k\right)}^{\prime }=k{x}^{k-1}\\ {\left(e^x\right)}^{\prime }=e^x;{\left(a^x\right)}^{\prime }=a^x\ln a,a>0,a\ne 1\\ (\ln x{)}^{\prime }=\frac{1}{x}(x>0);{\left({\log }_{a}x\right)}^{\prime }=\frac{1}{x\ln a},a>0,a\ne 1\\ (\sin x{)}^{\prime }=\cos x;(\cos x{)}^{\prime }=-\sin x\\ (\tan x{)}^{\prime }={\sec }^{2}x=\frac{1}{{\cos }^{2}x};(\cot x{)}^{\prime }=-{\csc }^{2}x=-\frac{1}{{\sin }^{2}x}\\ (\sec x{)}^{\prime }=\sec x\tan x;(\csc x{)}^{\prime }=-\csc x\cot x\\ (\arcsin x{)}^{\prime }=\frac{1}{\sqrt{1-x^2}};(\arccos x{)}^{\prime }=-\frac{1}{\sqrt{1-x^2}}\\ (\arctan x{)}^{\prime }=\frac{1}{1+x^2};(\mathrm{arccot}x{)}^{\prime }=-\frac{1}{1+x^2}\\ {\left[\ln \left(x+\sqrt{x^2+1}\right)\right]}^{\prime }=\frac{1}{\sqrt{x^2+1}};{\left[\ln \left(x+\sqrt{x^2-1}\right)\right]}^{\prime }=\frac{1}{\sqrt{x^2-1}}\end{array}$$

反函数

$$\begin{array}{lcc}x=f(t)& ,& y=g(t)\\ \frac{dy}{dx}& =& \frac{dy/dt}{dx/dt}=\frac{f^{\prime }}{g^{\prime }}\\ \frac{d^{2}y}{d{x}^2}& =& \frac{d(\frac{dy}{dx})}{dx}=\frac{d(\frac{dy}{dx})/dt}{dx/dt}=\frac{f^{\prime \prime }{g}^{\prime }-f^{\prime }{g}^{\prime \prime }}{(g^{\prime }{)}^3}=\frac{-y^{\prime \prime }}{(y^{\prime }{)}^3}\end{array}$$

曲率

$$k=\frac{|y^{\prime \prime }|}{[1+(y^{\prime }{)}^2{]}^{1.5}}$$

曲率半径

$$R=\frac{1}{k}$$

多元微分

无条件极值

$$\begin{gathered} \{\begin{array}{l}{f}^{\prime \prime }{}_{xx}\left(x_0,y_0\right)=A\\ f^{\prime \prime }{}_{xy}\left(x_0,y_0\right)=B\\ f^{\prime \prime }{}_{yy}\left(x_0,y_0\right)=C\end{array} \\ \Delta =B^2-AC\{\begin{array}{l}<0\text{极值}\{\begin{array}{l}A<0\text{极大值}\\ A>0\text{极小值}\end{array}\\ >0\text{不是极值}\\ ==0\text{失效}\end{array} \end{gathered}$$

曲面的法向量

$$(F_x^{\prime },F_y^{\prime },F_z^{\prime })$$

微分方程

分数型代换

$$\begin{array}{rl}& \frac{dy}{dx}=\varphi (\frac{y}{x})\\ & u=\frac{y}{x},t=ux,\frac{dy}{dx}=u+x\frac{du}{dx}\\ & \frac{du}{\varphi (u)-u}=\frac{dx}{x}\end{array}$$

伯努利

$$\begin{array}{rl}& y^{-n}\ast y^{\prime }+p(x)y^{1-n}=q(x)\\ & z=y^{1-n},\frac{dz}{dx}=(1-n)y^{-n}\frac{dy}{dx}\\ & \frac{1}{1-n}\frac{dz}{dx}+p(x)z=q(x)\end{array}$$

欧拉方程

可降阶

常系数微分方程

See：常系数微分方程

空间几何

三向量共面：$r(\vec{a},\vec{b},\vec{c})<3$，或者说行列式为0

点到直线距离：$\frac{|\overrightarrow{P_{0}P}|}{\vec{l}}$

直线夹角：$cos\theta =\frac{|l_1\ast l_2|}{|l_1|\ast |l_2|}$

积分

基础

\int\sec{x}&=&\ln{|\sec{x} +\tan{x}|} \\ \int{\csc{x}} &=& \ln{|\csc x - \cot x|} \\ \int{\frac{dx}{\sqrt{a^2 - x^2}}} &=&\arcsin{\frac{x}{a}}\\ \int{\frac{dx}{a^2 + x^2}} &=&\frac{1}{a}\arctan{\frac{x}{a}}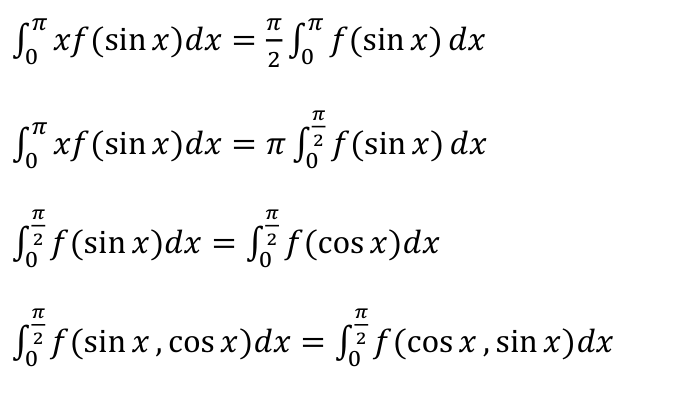

几何应用

面积

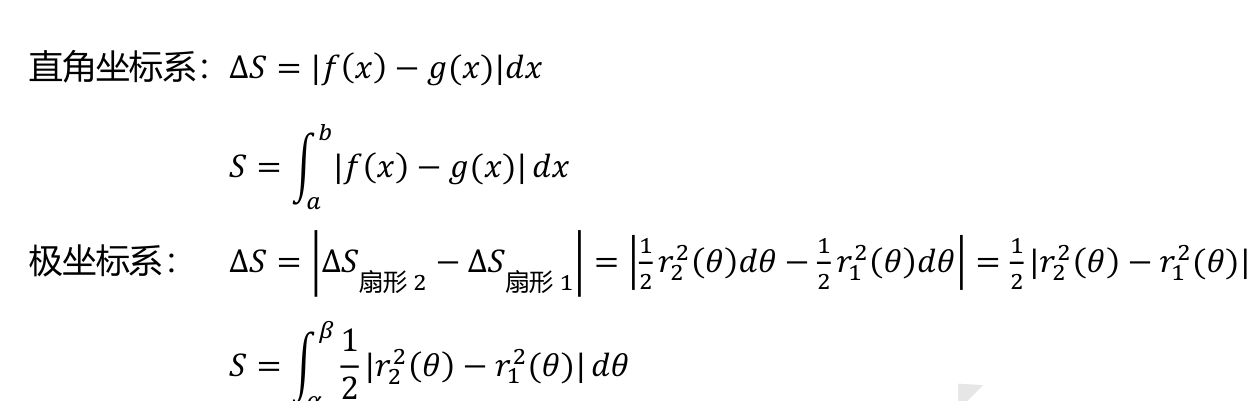
旋转体体积

弧长

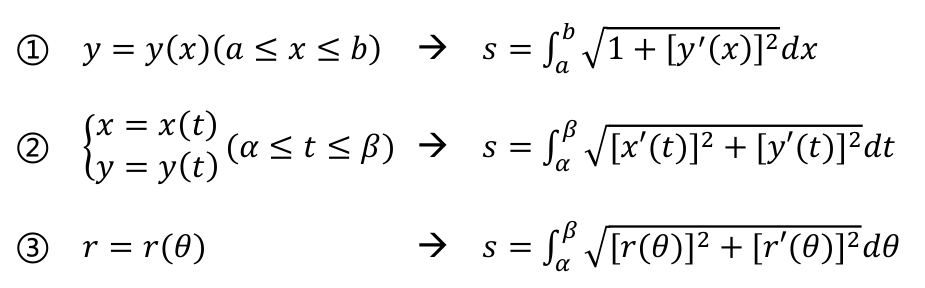
旋转曲面面积

级数

傅里叶级数

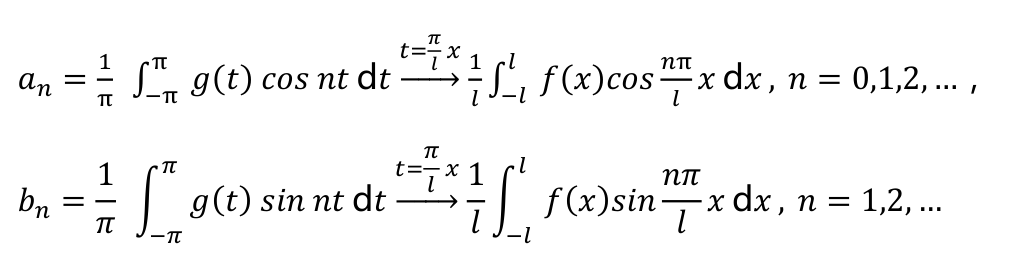
泰勒级数

线面积分

转动惯量

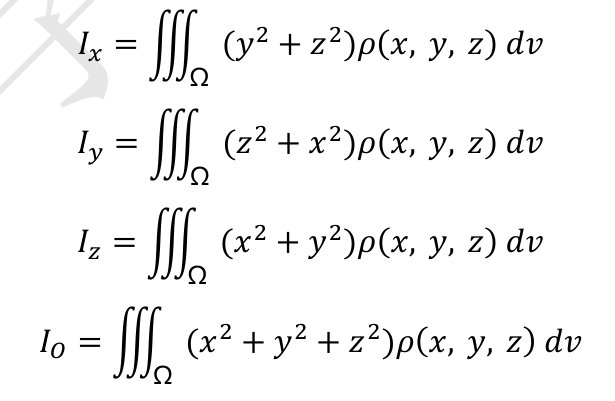
第一类曲线积分（空间曲线质量）

第一类曲面积分（空间曲面质量）

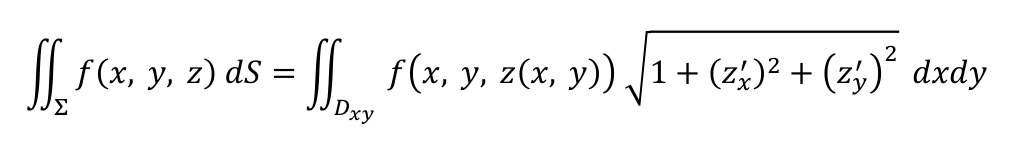
第二类曲线积分（向量积分，二维）

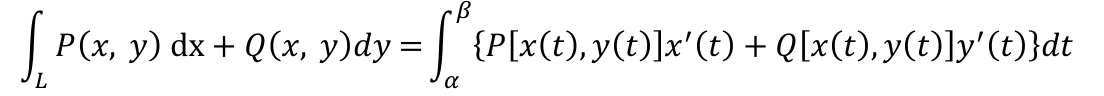
第二类曲面积分（求曲面通量）

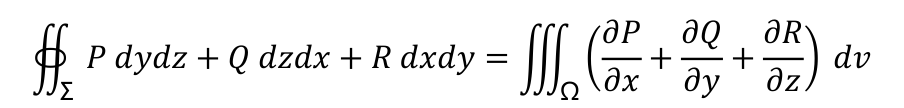
空间第二型曲线积分（向量积分，三维）斯托克斯公式