相关系数
相关概念:
总体:所要考察对象的全部个体。
样本:从总体中所抽取的一部分个体叫做总体的一个样本
可以样本统计量来估计总体统计量
皮尔逊person相关系数
概要
如果两组数据X:\{X_1,X_2,...,X_n\}$$Y:\{Y_1,Y_2,...,Y_n\}是总体数据
那么总体均值:,
总体协方差:
直观理解协方差:
- 如果X、Y变化方向一直相同,那么协方差为正
- 如果X、Y变化分享一直相反,那么协方差为负
- 其他情况下正负抵消
协方差大小与量纲有关,不适合作比较
\textcolor{red}{总体Person相关系数}$$\textcolor{red}{p_{xy}=\frac{Cov(x,y)}{σ_xσ_y}}=\frac{\sum_{i=1}^n{\frac{x_i-E(x)}{σ_x}}{\frac{y_i-E(y)}{σ_y}}}{n}其中均为大写
σ(sigma X)是X的标准差:,
可以证明:,且当时,
\textcolor{red}{样本Person相关系数}$$r_{x y}=\frac{Cov(X,Y)}{S_X S_Y}
(sigma X)是X的样本标准差,,
必须先确定两变量线性相关,才能使用Person相关系数
相关性可视化
通过绘制散点图判断X,Y之间的相关性
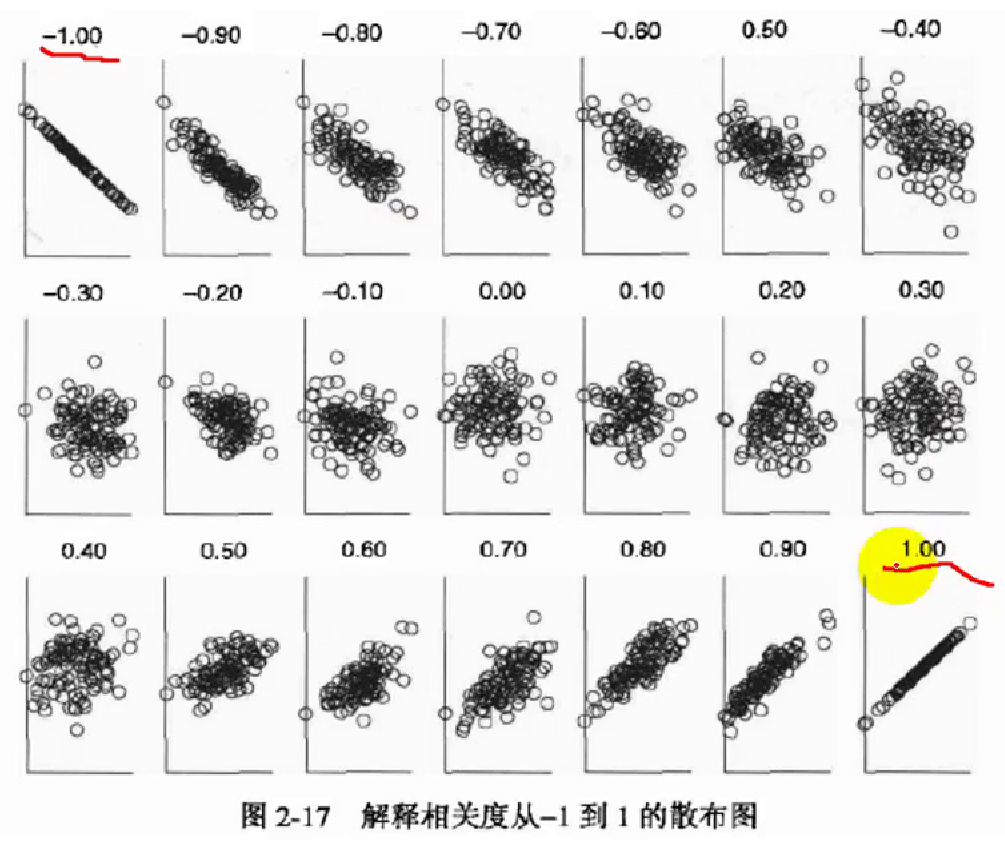
理解误区
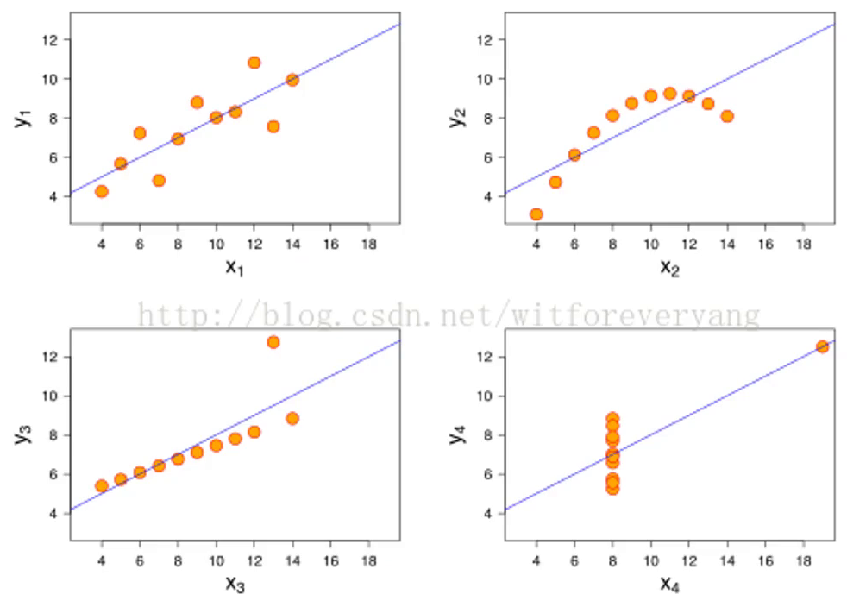
四图得出person相关系数均为0.816
-
非线性相关也会导致相关系数很大
-
离群点对相关系数影响很大,图3
-
两变量相关系数很大也不能说明两者相关,可能收到了异常值的影响,图4
冰淇淋销量与温度间关系

相关系数为0 TAT
- 相关系数结果为0,只能说不是线性相关,可能有复杂关系,图5
总结:Person相关系数反映的是线性相关系数,一定要画散点图QAQ
相关系数参考表
不可信,其更依赖实际背景和目的
| 相关性 | 其绝对值 |
|---|---|
| 无相关性 | 0.0-0.09 |
| 弱相关性 | 0.1-0.3 |
| 中相关性 | 0.3-0.5 |
| 前相关性 | 0.5-1.0 |
假设检验
小明之前都是90斤,今天称发现94斤
α: 显著性水平(又指犯第一类错误的概率,我们有多大可能性拒绝原假设)
: 置信水平,根据原假设成立的概率。
First:确立原假设 和 备择假设
检查小明体重W是不是为45,:W=45,:W45;
Second:在原假设成立的条件下,根据我们要检验的量构造一个分布
:W=45,W~N(45,4)
正态分布标准化:~N(0,1)
Third:画出分布的概率密度图
Then:给出置信水平