数学建模算法与应用

[TOC]

线性规划

线性规划问题

定义：线性规划就是在一系列线性条件的约束下，求一线性目标函数最值的问题

一般线性规划问题的标准型为：

$$maxz=\sum _{j=1}^n{c}_j{x}_j\text{\hspace{1em}(1)}$$ $$s.t.\{\begin{array}{r}\sum _{j=1}^n{a}_{ij}{x}_j=b_i,i=1,2,...,m\\ 0\le x_j,j=1,2,...,m\end{array}\text{\hspace{1em}(2)}$$

其中$b_i\ge 0,i=1,2,...,m$

可行解：满足 (2) 中条件的解 $x=[x_1,x_2,...,x_n{]}^T$, 称为线性规划问题的可行解，可使目标函数 (1) 达到最大值的可行解称为最优解

可行域：所有可行解构成的集合称为问题的可行域，记作$R$

Matlab标准型为:

$$\begin{gathered} mi{n}_x{f}^{T}x \\ s.t.\{\begin{array}{r}A\ast x\le b\\ Aeq\ast x=beq\\ lb\le x\le ub\end{array} \end{gathered}$$

式中 $f,x,b,beq,lb,ub$为列向量, $f$称为价值向量, $b$称为资源向量, $A，Aeq$为矩阵

Matlab中求解线性规划的命令为

[x,fval] = linprog(f,A,b)
% or
[x,fval] = linprog(f,A,b,Aeq,beq)
% or
[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)
 
% x返回决策向量的取值
% fval返回目标函数的最大值
% lb 和 ub 对应决策向量的 下界向量 和 上界向量

例:

$$\begin{gathered} maxz=2x_1+3x_2-5x_3, \\ {x}_1+x_2+x_3=7, \\ s.t.\{\begin{array}{r}2x_1-5x_2+x_3\ge 10,\\ x_1+3x_2+x_3\le 12\end{array} \\ {x}_1,x_2,x_3\ge 0 \end{gathered}$$

c = [-2,-3,5];
a = [-2,5,-1;1,3,1];
b = [-10;12];
aeq = [1,1,1];
beq = 7;
% zeros() 返回三行一列的为零向量
[x,y] = linprog(c,a,b,aeq,beq,zeros(3,1));
x, y = -y

将问题转化为线性规划问题

对于类型

$$\begin{gathered} min\sum _{i=1}^n|x_i| \\ s.t.Ax\le b \end{gathered}$$

取

$$\begin{gathered} u_i=\frac{x_i+|x_i|}{2} \\ {v}_i=\frac{|x_i|-x_i}{2} \end{gathered}$$

问题将转化为

$$\begin{gathered} min\sum _{i=1}^n(v_i+u_i) \\ s.t.\{\begin{array}{r}\left[\text{matrix}A,-A\right]\left[\text{matrix}u \\ v\right]\le b\\ u,v\ge 0\end{array} \end{gathered}$$

例：

$$\begin{gathered} minz=|x_1|+2|x_2|+3|x_3|+4|x_4| \\ s.t.\{\begin{array}{r}{x}_1-x_2-x_3+x_4\le -2\\ x_1-x_2+x_3-x_4\le -1\\ x_1-x_2-2x_3-3x_4\le -\frac{1}{2}\end{array} \end{gathered}$$

c=1:4;c = [c,c]';% 构造价值向量
a = [1 -1 -1 1;1 -1 1 -3;1 -1 -2 3];
a = [a,-a];
b = [-2 -1 -1/2];
[y,z] = linprog(c,a,b,[],[],zeros(8,1));
x = y(1:4)-y(5:end) %变换为原问题的解 x = u-v

投资的收益与风险

问题提出

市场上有$n$种资产$s_i,i=1,2,...,n$可供选择，现用数额为$M$的相当大的资金做投资。

$n$种资产中同一时期内购买$s_i$的平均收益率为$r_i$，风险损失率为$q_i$，投资越分散，总风险越少，所以投资风险可由最大风险代替。

符号规定与基础假设

符号规定：

1. $s_i$表示第$i$个投资项目，$i=0,\mathrm{1...},n$，$s_0$表示存入银行
2. $r_i$，$p_i$，$q_i$分别表示$s_i$的平均收益率、交易费率、风险损失率，$i=0,1,...,n$，其中$p_0=0$、$q_0=0$
3. $u_i$表示$s_i$的交易定额，$i=1,2,...n$
4. $x_i$表示投资项目$s_i$的资金，$i=0,\mathrm{1...},n$
5. $a$表示投资风险度
6. $Q$表示总体收益

基本假设：

1. $M$极大，一般为1
2. 投资越分散，总风险越少
3. 所以投资风险可由最大风险代替
4. $n+1$种资产相对独立

模型建立

总体风险由$s_i$中最大的代替，即：

$$max\{q_i{x}_i|i=1,2,...,n\}\text{\hspace{1em}(1)}$$

购买$s_i(i=1,2,...,n)$所付的交易费为一分段函数，即

$$交易费=\{\begin{array}{r}{p}_i{x}_i,x_i>u_i\\ p_i{u}_i,x_i\le u_i\end{array}\text{\hspace{1em}(2)}$$

要使净收益率尽可能大，总体风险尽可能小，so这个是多目标规划模型

目标函数为

$$\{\begin{array}{r}max\sum _{i=0}^n(r_i-p_i)x_i\\ min\{\underset{1\le i\le n}{\max }\{q_i{x}_i\}\}\end{array}$$

约束条件

$$\{\begin{array}{r}\sum _{i=0}^n(1+p_i)x_i=M\\ x_i\ge 0,i=0,\mathrm{1...},n\end{array}$$

模型简化

模型一：

固定风险水平，优化收益

若给定能风险界限为$a$，即$\frac{q_i{x}_i}{M}\le a(i=1,2,...,n)$

$$\begin{gathered} \max \sum _{i=0}^n(r_i-p_i)x_i, \\ s.t.\{\begin{array}{r}\frac{q_i{x}_i}{M}\le a,i=1,2,...,n\\ \sum _{i=0}^n(1+p_i)x_i=M\end{array} \end{gathered}$$

模型二：

固定盈利水平，最小化风险

设定总盈利至少达到$k$以上，寻找风险最小的投资组合

$$\begin{gathered} \min \{\underset{1\le i\le n}{\max }\{q_i{x}_i\}\} \\ s.t.\{\begin{array}{r}\sum _{i=0}^n(r_i-p_i)x_i\ge k\\ \sum _{i=0}^n(1+p_i)x_i=M\\ x_i\ge 0,i=0,1,...,n\end{array} \end{gathered}$$

模型三：

对风险、收益赋予权重$s(0<s\le 1)$和$1-s$。$s$称为投资偏好系数。

$$\begin{gathered} min\{s\{\underset{1\le i\le n}{\max }\{q_i{x}_i\}\}-(1-s)\sum _{i=0}^n(r_i-p_i)x_i\} \\ s.t.\{\begin{array}{r}\sum _{i=0}^n(1+p_i)x_i=M,\\ x_i\ge 0,i=0,1,2,...,n\end{array} \end{gathered}$$

模型求解

% 模型1 的求解
a=0;
hold on;
while a<0.05
   c=[-0.05, -0.27,-0.19,-0.185,-0.185];
   A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];
   b=a*ones(4,1);
   Aeq=[1,1.01,1.02,1.045,1.065];
   beq =1;
   LB = zeros(5,1);
   [X,Q] = linprog(c,A,b,Aeq,beq,LB);
   Q=-Q;
   plot(a,Q,'*k');
   a=a+0.001;
end
xlabel('a'),ylabel('Q')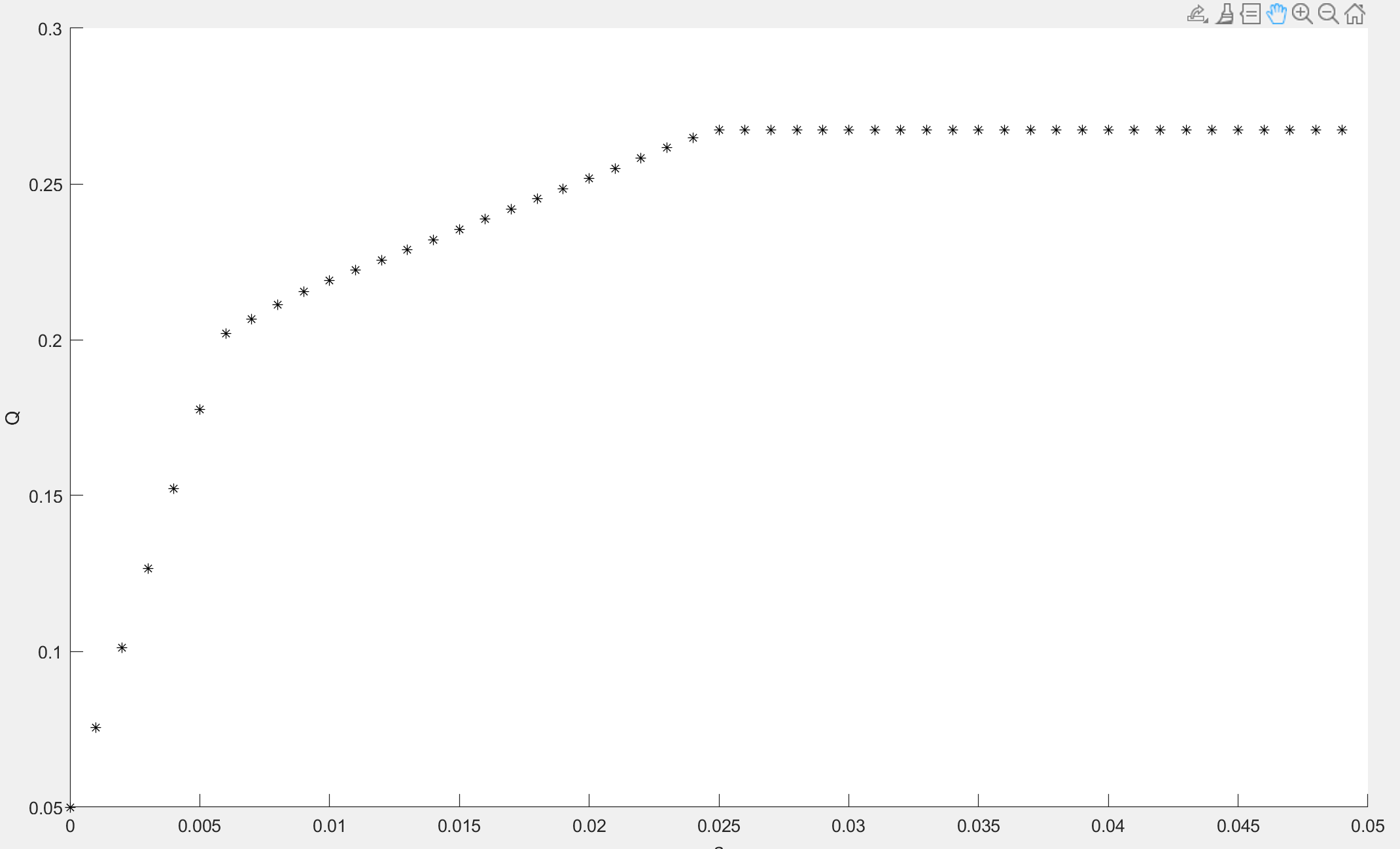

习题

1

$$\begin{gathered} maxz=3x_1-x_2-x_3 \\ s.t.\{\begin{array}{r}{x}_1-2x_2+x_3\le 11,\\ -4x_1+x_2+2x_3\ge 3\\ -2x_1+x_3=1\\ x_1,x_2,x_3\ge 0\end{array} \end{gathered}$$

% 转化为2个变量
c = [-1,1];
a = [3,-2];
b = [10];
lb = [0,1];
[x,fval] = linprog(c,a,b,[],[],lb);
 x = [x; (2*x(1)+1)],fval = -fval+1

2

$$\begin{gathered} minz=|x_1|+2|x_2|+3|x_3|+4|x_4| \\ s.t.\{\begin{array}{r}{x}_1-x_2-x_3+x_4=0,\\ x_1-x_2+x_3-3x_4=1\\ x_1-x_2-2x_3+3x_4=-\frac{1}{2}\end{array} \end{gathered}$$

c=1:4;c = [c,c]';% 构造价值向量
 
aeq = [1,-1,-1,1;1,-1,1,-3;1,-1,-2,3];
beq = [0,1,-1/2];
aeq = [aeq,-aeq];
[ul,fval] = linprog(c,[],[],aeq,beq,zeros(8,1));
x = ul(1:4)-ul(5:end),fval

3

设备	产品			有效台时	满负荷时设备费用/元
	I	II	III
A1	5	10		6000	300
A2	7	9	12	10000	321
B1	6	8		4000	250
B2	4		11	7000	783
B3	7			4000	200
原料费(元/件)	0.25	0.35	0.5
单价(元/件)	1.25	2	2.8

4

整数规划

非线性规划

图与网络模型及方法

插值与拟合

微分方程建模

数理统计

时间序列

支持向量机

多元分析

偏最小二乘回归分析

现代优化算法

数字图像处理

综合评价与决策方法

预测方法

目标规划