范围最小查询(Range Minimize Query)问题如下:给定一个数组,对其进行预处理,以便高效地确定各种子范围内的最小值。RMQ 在计算机科学领域有大量应用,是许多高级算法技术的绝佳试验场。通过使用一种名为笛卡尔树的新数据结构和一种名为四俄方法的技术,我们实现了 RMQ 的⟨O(n)、O(1)⟩-time 解决方案。我们可以调整我们的方法,最终得到一个预处理时间、查询时间的 RMQ 解决方案。在此过程中,我们将看到许多在数据结构设计中会反复出现的巧妙技术。
问题描述
给定任意数组 ,对于任意 请给出区间 的最小值

Solutions
硬算
直接从 i 到 j 遍历,找到最小的
时间复杂度: 空间复杂度:
但是我们宁愿多花点时间用于构造,省下时间来查询,因为查询可能有很多次。
空间换时间 - 打表
提前记录每个查询,到查询时再找
对于长度为的数组,一共有个可能的RMQ查询,那么我们可以将所有的查询都记录下来,然后每次以的复杂度得出答案。
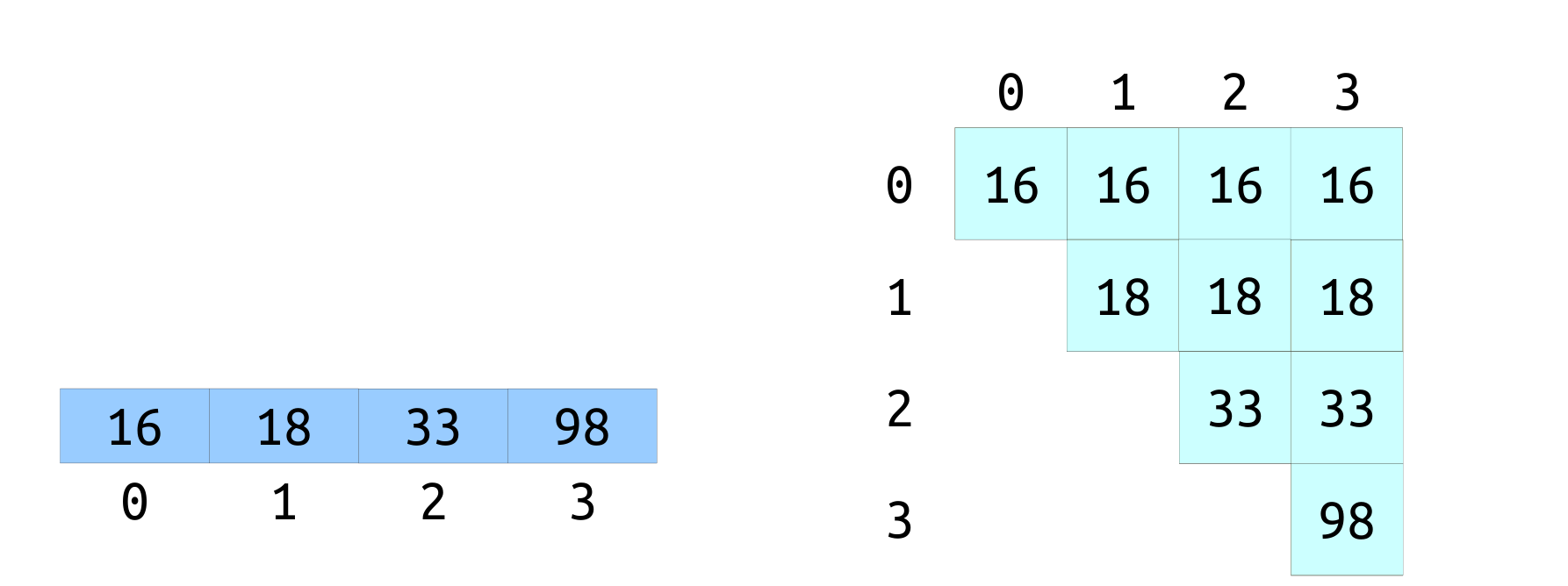 时间复杂度:,但是构建时间
空间复杂度:
时间复杂度:,但是构建时间
空间复杂度:
这里可以使用动态规划加速:
首先只考虑对角线上的元素,然后从对角线元素推导出其他查询的结果。 即初始化
dp[i][i] = a[i][i], 然后由状态转移方程:dp[i][j] = min(dp[i][j-1], dp[i+1][j])快速计算 总的复杂度为

时间复杂度:,构建时间 空间复杂度:
分而治之 - Block Decomposition
将元素数组分成 个桶,每个桶里面求出最小值。
查询时:如果横跨整个桶,就按记录的桶中最小值来,反之还是要计算的。

- 时间复杂度:,时间查询整个桶,查询分桶的
- 构建时间:
- 空间复杂度:
- 最佳的: ,这时时间复杂度:
Sparse Tables(ST表) - 更小的空间
对于每个索引 ,计算从 开始的范围的RMQ,大小为1、2、4、8、16、…、,直到越界
观察下面整个情况,2-7之间的最小值可以通过两个更小的,长度为的子问题求出来:RMQ[2,7] = min(RMQ[2,5], RMQ[4,7])
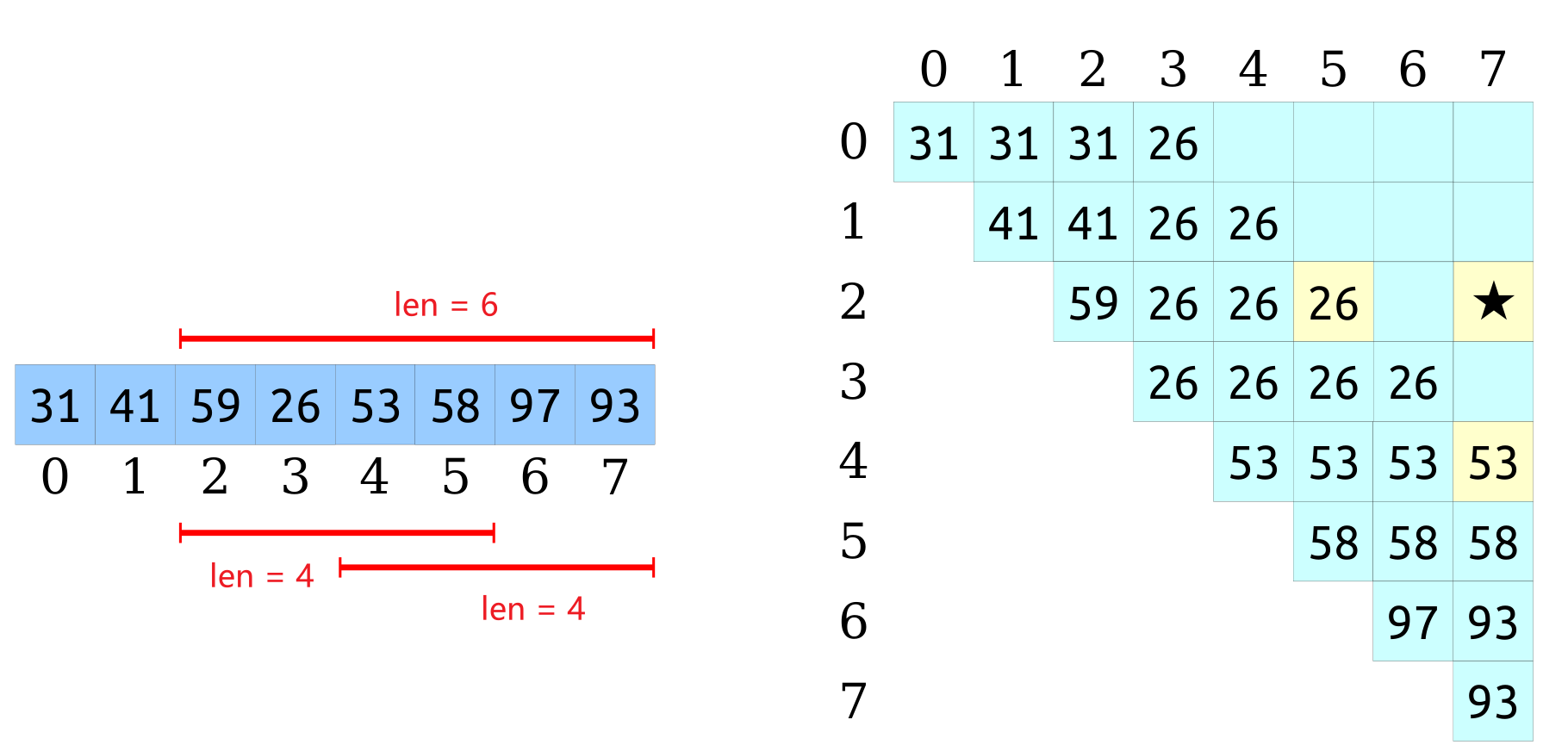
那么只需要可以一个更小的备忘录来辅助查询
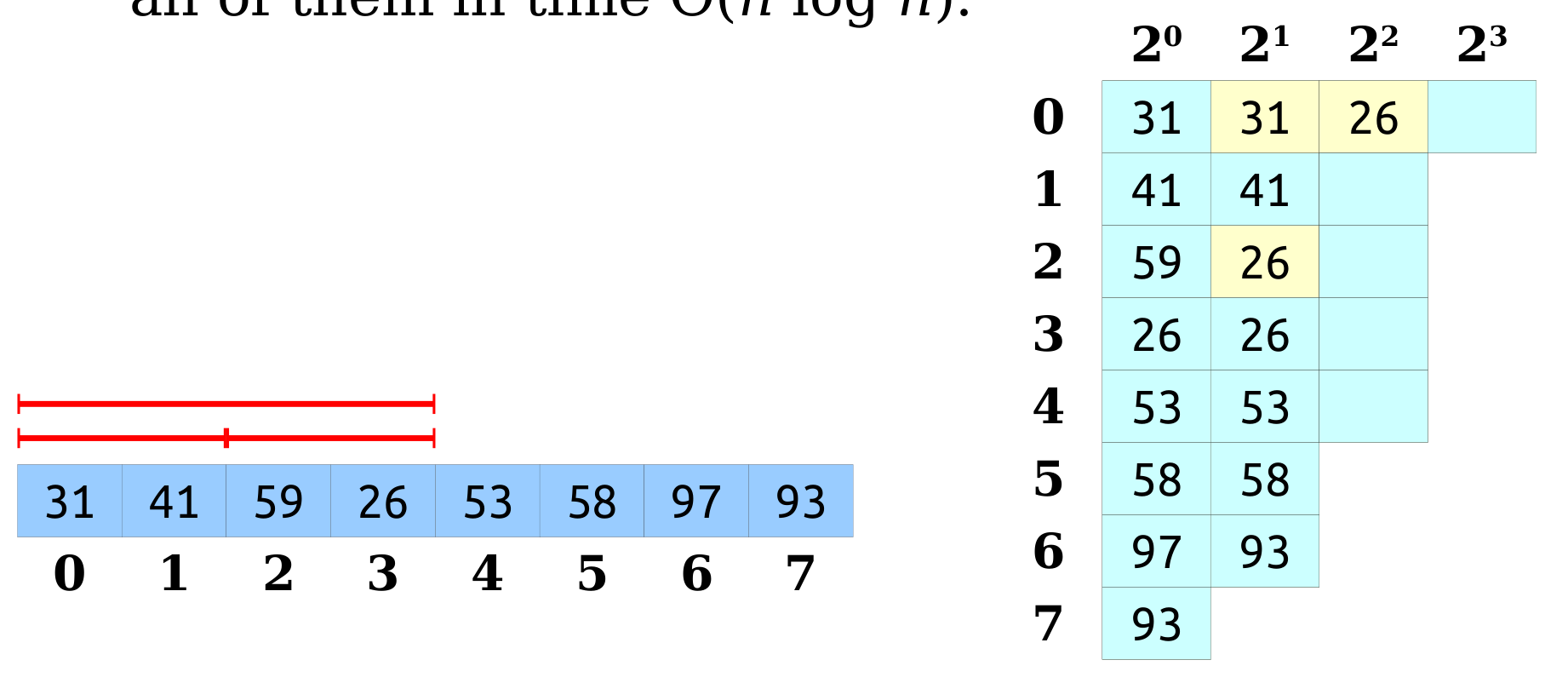
todo 这个备忘录保存了从i开始长度为的子数组的最小值,而且这个备忘录也可以用动态规划求解出来。
时间复杂度:,构建
空间复杂度:
组合查询
采用分桶的思想,将整个数组的RMQ分解成几个子RMQ,父子RMQ问题会采用不同的策略(比如线性,sparse),甚至父子RMQ问题都可以采用组合查询。

我们采用记号 分别表示父子查询的构建耗时和单次查询耗时。(p=precompute,q=query)
那么组合查询的查询复杂度为 ,总构建时间 ,通过组合可构造出更小复杂度的算法
一些组合例子
比如组合sparse与线性
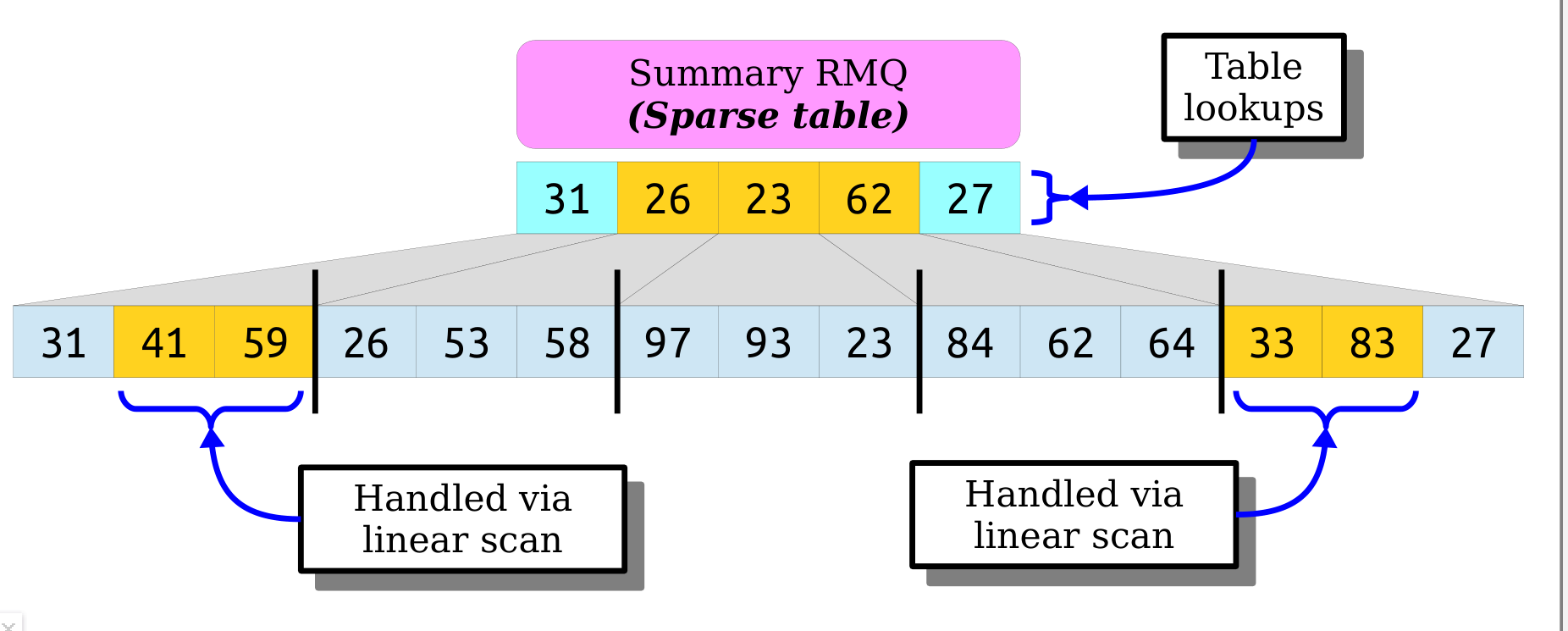
构建:,查询
全用sparse

构建:,查询
笛卡尔树
笛卡尔树可以在 的复杂度上解决RMQ问题。
问题转换
组合查询的查询复杂度为 ,总构建时间 ,记作
那么如果要构建复杂度为 的算法, 和 的复杂度为多少?
于是问题转换为:
能否在 时间构建数据结构,满足在很多个子数组中查询最小值下标,且查询时间复杂度为 。(这里可以把单个数字看作长度为1的数组
为什么这个问题会比之前的问题更简单?举个例子:
两个数组
1 3 2 4
10 30 20 40
11 31 21 41
100 300 200 400
166 361 261 464
无论你如何选择i,j,返回下标都一样!!!
这意味者RMQ问题在这两个数组上是等价的,返回的坐标相同,这里我们记作RMQ结构相同。
那么子RMQ问题就可以转换成有限个更小的RMQ问题,比如下面这个图。

如何判断RMQ结构是否相同
假设数组 B1 B2 长度都为 b,只要他们满足
就称其等价,记作
只要 ,那么最小值下标就相同,而且可以递归的应用到子数组上!
笛卡尔树结构如下:
- 树的根是数组的最小元素。
- 它的左右子树是通过递归构建形成的
- 笛卡尔树的子数组的左、右最小值。
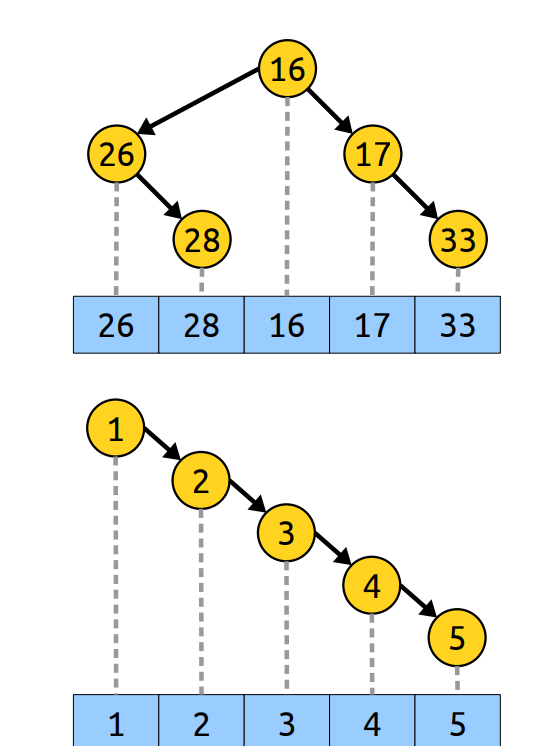
那么是不是只要笛卡尔树形状相同,就可以说明俩数组等价啦
构建
构建复杂度如下:
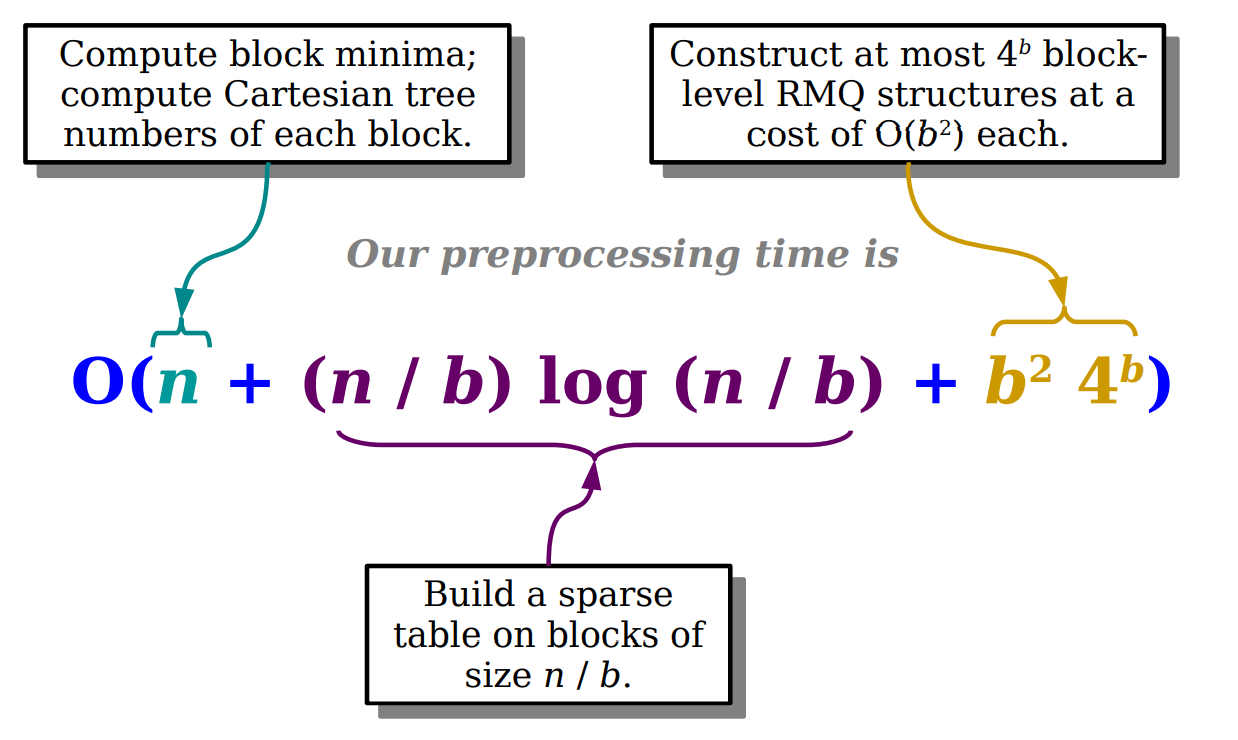
计算最小值,数组长为 的笛卡尔树一共 种,当 且 时复杂度不超过 ,总体复杂度
查询

线段树
树状数组
例题
参考
- Slides:
- Part One
- Part Two:
- 论文阅读:Guibas, Leo and Sedgewick, Robert. A Dichromatic Framework for Balanced Trees