k select problem

PDF

description

function: Select(A, k) Input: array A of $n$ numbers, and an integer $k\in 1,...,n$. Output: the k-th smallest number in A.

一种方法就是先排序然后选择第k个，时间复杂度O(nlog(n))

Solution

stanford 笔记地址 PDF

从特殊到一般：

最小元素(k=1)

非常直接的思路就是逐个遍历然后更新最小值，时间复杂度O(n) 这谁都会嘛 :D

第二小元素(k=2)

还是很简单，使用两个参数存最小的和第二小的不就行了吗？

中位数(k=$\frac{n}{2}$)

这时候，如果使用数组的话，我们就进入了一个插入排序的陷阱，复杂度就会上升到O(n^2)了

分治

思路

1. 我要第 $k$ 个最小的，关你后 $n-k$ 个最大的什么事？
2. 我要第 $k$ 个最小的，不需要知道它之前的元素顺序

可以想办法从逻辑上去除(忽略)后 $n-k$ 个最大的。怎么去除呢？

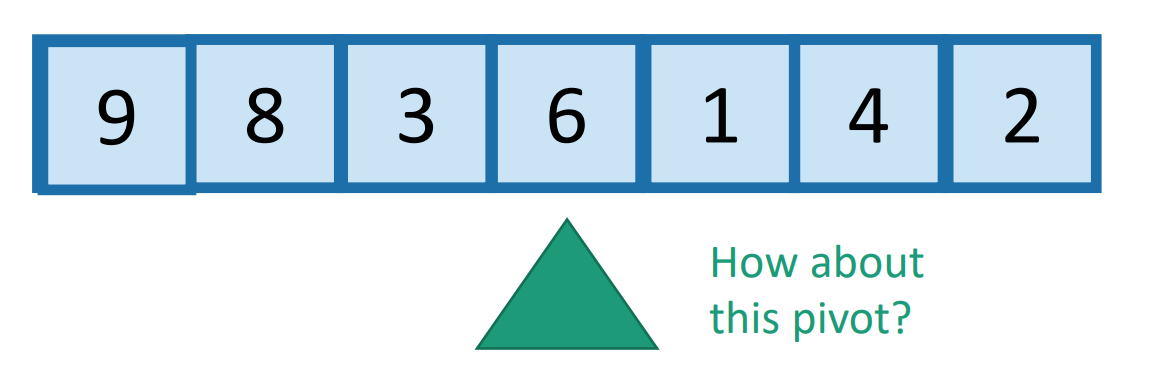可以随便选择一个点pivot，让小于这个点的移到左边，大于的移到右边（复杂度O(n)）

假设把 $a_{<}$ 个元素划分到了左边，划分到左边的数组记作 $A_{<}$ ，划分到右边的记作 $A_{>}$，那么问题就转换为了子问题：

• select(A,k)
  • pivot, $a_{<}=k-1$
  • select($A_{<}$, k), $a_{<}>=k$
  • select($A_{>}$, $k-a_{<}-1$), $a_{<}<k$

复杂度分析

整个程序的复杂度如下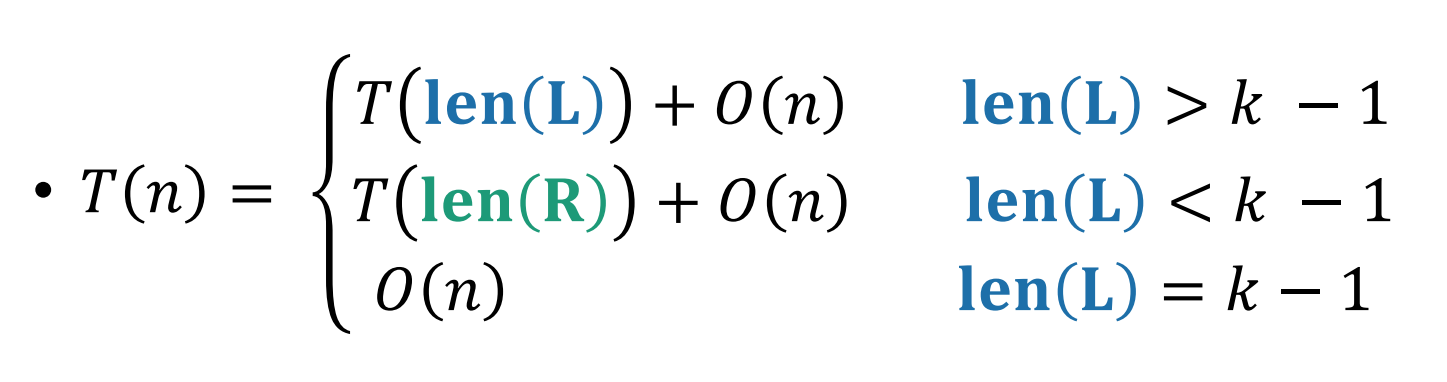： 这里的 len(L/R) 表示划分后数组大小。

• 在理想情况下，每次都将数组切成两半，那么用主定理算出来复杂度是$O(n)$
  • $T(n)=T(n/2)+O(n)$
• 在最差情况下（每次都选到最大/最小值），复杂度就是O(N^2)了
  • $T(n)=T(n-1)+O(n)$

pivot选取

至于pivot怎么选择，其实只要运气不太差，复杂度就还是O(n)的。这个差运气的概率为 $\frac{1}{n!}$，除非测试用例故意搞你，几乎不可能发生:P

cs161给出的做法是划分几个小区快，从这些区块中选择 povit*，在这些 povit*中选择最终的 povit