项目内容

About

cpp implementation of Bloom Filter, Shifting Bloom Filter, Spatial Bloom Filter, and other variants like partition filter, dynamic filter.

Todo Lists

Installation

#include"bf.h"
using namespace filter;

数据结构

过滤器基类

我定义过滤器基类可以

添加元素
查询元素存在性
打印内部信息（可删除）

class BaseFilter
{
public:
	virtual void add(uint64_t key) = 0;
	virtual bool query(uint64_t key)const = 0;
	virtual std::string to_string() const = 0;
	virtual ~BaseFilter(){}
};

经典布隆过滤器

Bloom过滤器是一种空间效率的概率数据结构，由Burton Howard Bloom在1970年提出，用于测试一个元素是否是集合的成员。假阳性匹配是可能的，但假阴性不可能，只需要少量的内存就可以存储大量的信息

A picture from Prefix Filter Picture is From:The Prefix Filter: Practically and Theoretically Better Than Bloom. VLDB 2022

Shifting Bloom Filter

布隆过滤器的改进版本，引入了 $o (e)$ 存储额外的信息，并且可以只通过一次 hash 同时设置两个 bit

References: T. Yang et al., “A shifting bloom filter framework for set queries,” Proc. VLDB Endow., vol. 9, no. 5, pp. 408–419, Jan. 2016, doi: 10.14778/2876473.2876476.

membership

使用一半的hash函数，然后额外取一个作为 offset，每次添加/查询元素 e 时将 $h_{i} (e)$ 和 $h_{i} (e) + o (e)$ 都设为1. 优点：同时访问两个bit 缺点：相同参数下，更高的误判率

association

专门用于集合查询的Shifting Bloom Filter，需要两个集合 $A, B$ ，根据元素 e 在 $A, B$ 中的存在情况不同，设定不同的offset。在查询时根据offset不同判断元素的存在信息。

Spatial Bloom Filter

References:

P. Palmieri, L. Calderoni, and D. Maio, “Spatial Bloom Filters: Enabling Privacy in Location-Aware Applications,” in Information Security and Cryptology, vol. 8957, D. Lin, M. Yung, and J. Zhou, Eds. Cham: Springer International Publishing, 2015, pp. 16–36. doi: 10.1007/978-3-319-16745-9_2.
作者官网：Spatial Bloom Filters
作者在线演示：live demo

Partition Bloom Filter

造成布隆过滤器误判的一大原因就是和其他hash冲突，可以将所有比特数组分成几个桶，每个桶单独一个hash，那么每一个hash函数只会和自己之前的hash冲突。

Reference: Chang, F., Feng, W. C., & Li, K. (2004, March). approximate caches for packet classification. In INFOCOM 2004. Twenty-third AnnualJoint Conference of the IEEE Computer and Communications Societies (Vol. 4, pp. 2196-2207). IEEE. (Full text article)

Scalable Bloom Filter

动态布隆过滤器，在内存允许的情况下可以存储理论无限的数据，不需要某个先验的最大输入规模。

下图展示了一个Scalable Bloom Filter的基本模型（下文简称SBF）。该SBF一共包含BF0和BF1两层。在一开始，SBF只包含BF0层，假设在插入a、b、c三个元素后，BF0层已经无法保证用户设定的误判率，此时会创建新的一层（BF1层）进行扩容。因此，后面的d、e、f元素会插入到BF1层中。同理，当BF1层也无法满足误判率时，会创建新的一层（BF2层），如此进行下去。Scalable Bloom Filter只会向最后一层插入数据，同时也从最后一层开始查询，直到查询至BF0层。

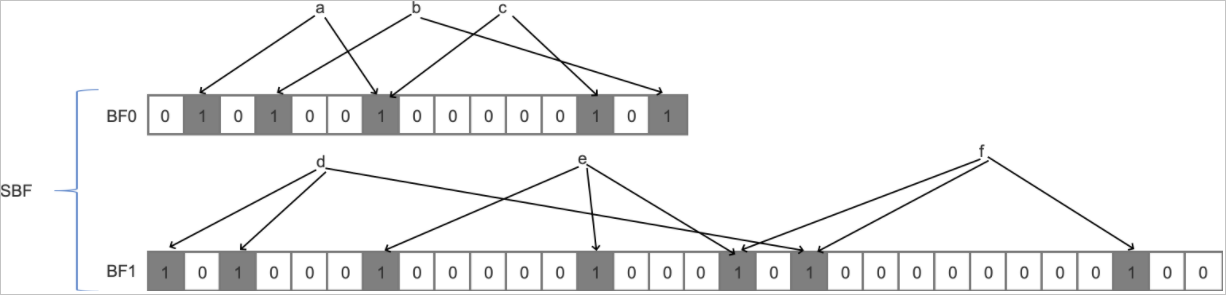
SBF模型

Reference: ALMEIDA, Paulo Sérgio, BAQUERO, Carlos, PREGUIÇA, Nuno, et al. Scalable bloom filters. Information Processing Letters, 2007, vol. 101, no 6, p. 255-261. (Full text article)

My Filter

Partition + Shifting

造成 shifting 错误率的一大原因就是和其他hash冲突，或者与其他hash的offset冲突，那么可以将其限定到一个桶里。在数据量较小时，冲突率会很大，但是当数据量达到 1e9 甚至 1e10 时桶中冲突的概率就会大大减小。

Spatial + Shifting + ID

Spatial一个area就占用1个或者2个byte，那么如果有255个area还好，利用率100%，但是在256时就得分配2个byte，这时候有7个bit没有用到，几乎浪费了一半的空间

ID bloom filter 可以提高空间利用率，它不再已byte为单位，而是看看最多几个bit能装下。因为，不再占用整数个字节，那么寻址也不是字节位置，为避免对原有信息产生影响，使用或运算而不是加法。
Shifting 将 offset 作为一个hash，这时候可以一次选择并处理两个 area（不是bit了）

Tests

数据集

def vis_dataset(file_path):
    df = pd.read_csv(file_path, sep=' ', nrows=int(1e6), header=None, names=['number', 'exists'])
    plt.hist(df['number'], 1000, histtype='step', density=True)
    plt.title(file_path.split('/')[1])
    plt.show()

正态分布

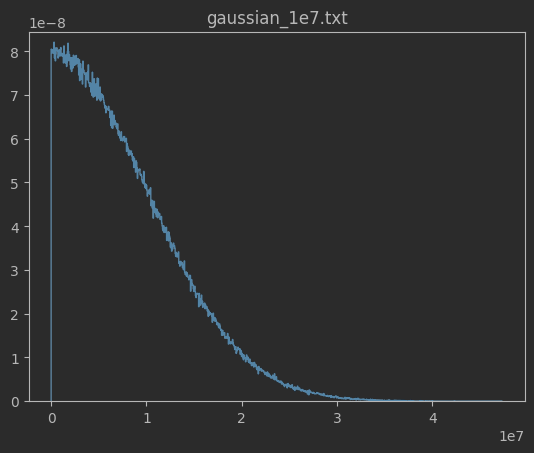
均匀分布

指数分布

False Positive Test

Performance Test

references

GitHub - Callidon/bloom-filters: JS implementation of probabilistic data structures: Bloom Filter (and its derived), HyperLogLog, Count-Min Sketch, Top-K and MinHash
T. Yang et al., “A shifting bloom filter framework for set queries,” Proc. VLDB Endow., vol. 9, no. 5, pp. 408–419, Jan. 2016, doi: 10.14778/2876473.2876476.
L. Calderoni, D. Maio, and P. Palmieri, “Bloom filter variants for multiple sets: a comparative assessment,” jucs, vol. 28, no. 2, pp. 120–140, Feb. 2022, doi: 10.3897/jucs.74230.
S. Z. Kiss, “Bloom Filter with a False Positive Free Zone,” p. 12.
H. Dai, “Bloom Filters and its Variants,” p. 90.
B. Mößner, C. Riegger, A. Bernhardt, and I. Petrov, “bloomRF: On Performing Range-Queries in Bloom-Filters with Piecewise-Monotone Hash Functions and Prefix Hashing,” p. 13.
S. Negi, A. Dubey, A. Bagchi, M. Yadav, N. Yadav, and J. Raj, “Dynamic Partition Bloom Filters: A Bounded False Positive Solution For Dynamic Set Membership (Extended Abstract).” arXiv, Jan. 19, 2019. Accessed: Nov. 16, 2022. [Online]. Available: http://arxiv.org/abs/1901.06493
M. G. Solomon, V. Sunderam, L. Xiong, and M. Li, “Enabling mutually private location proximity services in smart cities: A comparative assessment,” in 2016 IEEE International Smart Cities Conference (ISC2), Sep. 2016, pp. 1–8. doi: 10.1109/ISC2.2016.7580757.
P. Liu et al., “ID Bloom Filter: Achieving Faster Multi-Set Membership Query in Network Applications,” in 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, May 2018, pp. 1–6. doi: 10.1109/ICC.2018.8422627.
P. S. Almeida, C. Baquero, N. Preguiça, and D. Hutchison, “Scalable Bloom Filters,” Information Processing Letters, vol. 101, no. 6, pp. 255–261, Mar. 2007, doi: 10.1016/j.ipl.2006.10.007.
P. Palmieri, L. Calderoni, and D. Maio, “Spatial Bloom Filters: Enabling Privacy in Location-Aware Applications,” in Information Security and Cryptology, vol. 8957, D. Lin, M. Yung, and J. Zhou, Eds. Cham: Springer International Publishing, 2015, pp. 16–36. doi: 10.1007/978-3-319-16745-9_2.
T. M. Graf and D. Lemire, “Xor Filters: Faster and Smaller Than Bloom and Cuckoo Filters,” ACM J. Exp. Algorithmics, vol. 25, pp. 1–16, Dec. 2020, doi: 10.1145/3376122.
Bloom, B. H. (1970). Space/time trade-offs in hash coding with allowable errors. Communications of the ACM, 13(7), 422-426. (Full text article)

Quartz 4

Explorer