DFA

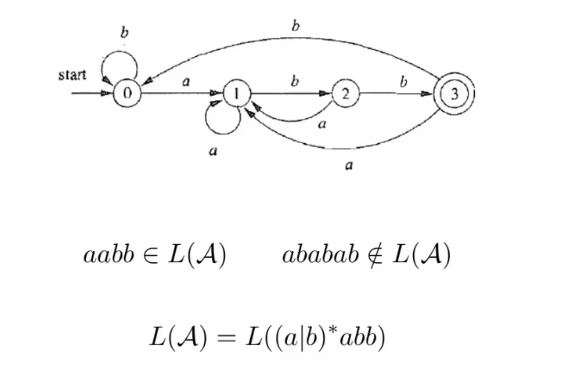
简介

Deterministic Finite State Machine（确定性有限状态机，DFSM）是有限状态机（Finite State Machine，FSM）的一种类型。在确定性有限状态机中，系统的每个状态都有唯一的出边与每个输入相关联，这意味着对于给定的输入和当前状态，系统有确定的下一个状态。简而言之，DFSM 的转移规则是确定的，不会存在多个可能的下一状态。

关键特征包括：

1. 唯一性： 对于任何给定的输入和当前状态，确定性有限状态机都有唯一的下一个状态。这使得系统的行为在给定输入下是可预测的。
2. 简单性： 由于唯一性的特性，确定性有限状态机在分析和实现上通常相对简单。状态转换表易于理解和实现。
3. 确定性转移函数： 确定性有限状态机的状态转移函数是确定性的，即对于每对（状态，输入）组合，只有一个可能的下一状态。

DFSM在许多应用中都非常有用，包括编程语言编译器的设计、通信协议的建模、硬件控制电路的设计等。由于其确定性，它们通常用于描述那些在给定输入下具有唯一响应的系统。

定义

NFA：确定的有穷状态机，组成是一个五元组 $A=(\Sigma ,S,s_0,\delta ,F)$

1. 字母表：$\Sigma$
2. 有穷状态集合：$S$
3. 唯一的初始状态： $s_0\in S$
4. 状态转移函数：$\delta :S\times \Sigma \to S$
5. 接受状态集合：$F\in S$

与NFA区别

1. 所有规定对应出边的字符默认指向一个死状态
2. 状态转移函数是确定的
3. NFA简洁易于理解，便于描述语言$L(A)$，DFA易于判断$x\in L(A)$，适合产生词法分析器。
   1. 因此在实际中，我们使用 RE => NFA => DFA => 做法分析器 的工作流

死状态

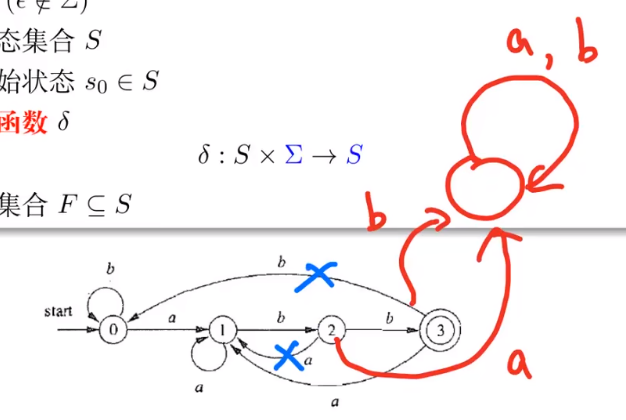
在有限自动机（DFA，Deterministic Finite Automaton）中，死状态是指一旦自动机进入该状态，它就无法再离开或接受任何输入。死状态通常是自动机设计中的一种特殊状态，表示自动机已经处于某种终止状态，不再接受任何输入，或者输入不再改变自动机的状态。

eg：如果删除某两条边，那么这两条表会指向一个死状态，这个死状态指向自身，因此永远循环下去。

DFA最小化

see：DFA最小化

例子