DFA最小化

如何定义等价状态

定义1

$s\sim t⟺\forall a\in \Sigma .\left((s\stackrel{a}{\to }{s}^{\prime })\wedge (t\stackrel{a}{\to }{t}^{\prime })\right)⟹(s^{\prime }=t^{\prime }).$

无论出现什么样的字符，我们都会走向同一个状态

但是这个假设是错的，以下图为例 ACE按照以上规则是等价的，但是其实不等价

定义2

更改定义，不需要转移到相同状态，而是转移到等价状态。

算法：不断合并等价状态，直到无法合并为止。

butw，这是一个递归定义，我们该从哪里开始呢？

所有接受状态等价吗

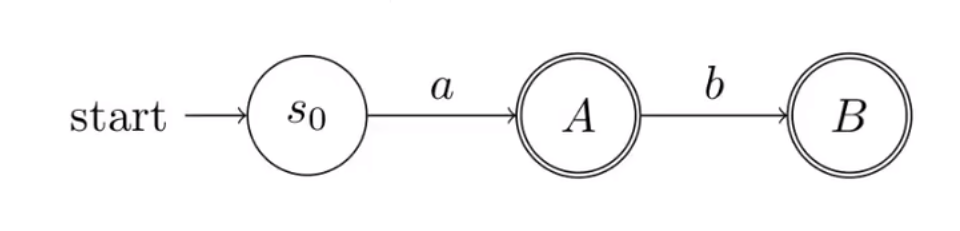不等价

Hopcroft的定义

不是合并状态，而是分裂状态

$$s\nsim t⟺\exists a\in \Sigma .\left(s\stackrel{a}{\to }{s}^{\prime }\right)\wedge \left(t\stackrel{a}{\to }{t}^{\prime }\right)\wedge \left(s^{\prime }\nsim t^{\prime }\right)$$

最开始所有的状态都等价，然后将肯定不等价的分开

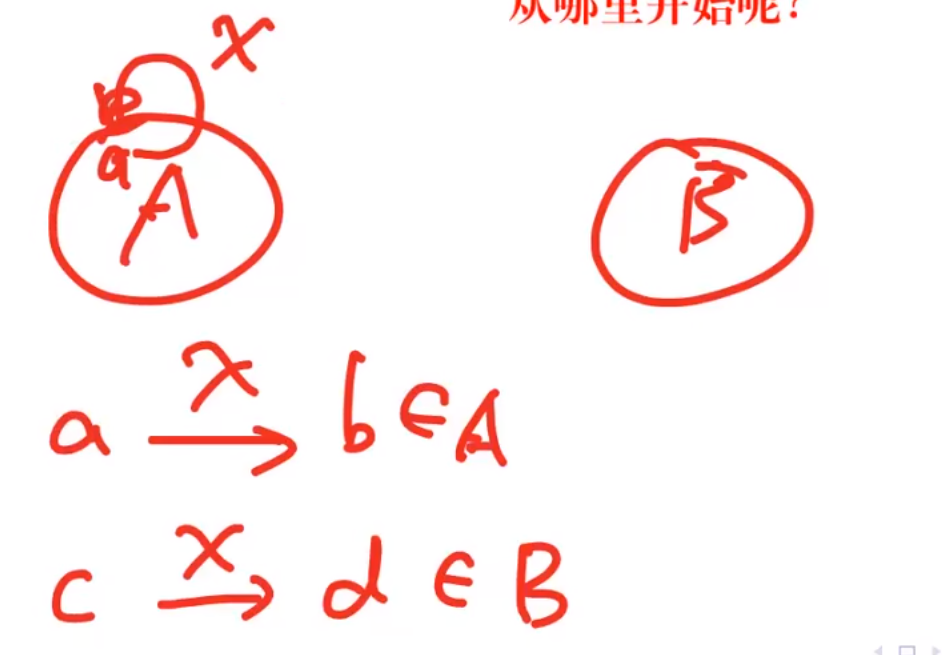
如何开始

所有的接受状态和非接受状态一定不等价： $\Pi =\{F,S\setminus F\}$

0. 最开始ABCDE等价，现在是：{ABCDE}
1. E是结束，将E分裂出来。现在是{ABCD}, {E}
2. D经过b进入E,现在是{ABC}, {D}, {E}
3. B经过b进入D，B分裂出来
4. AC区分不了，最小集合：{AC}, {B}, {D}, {E}

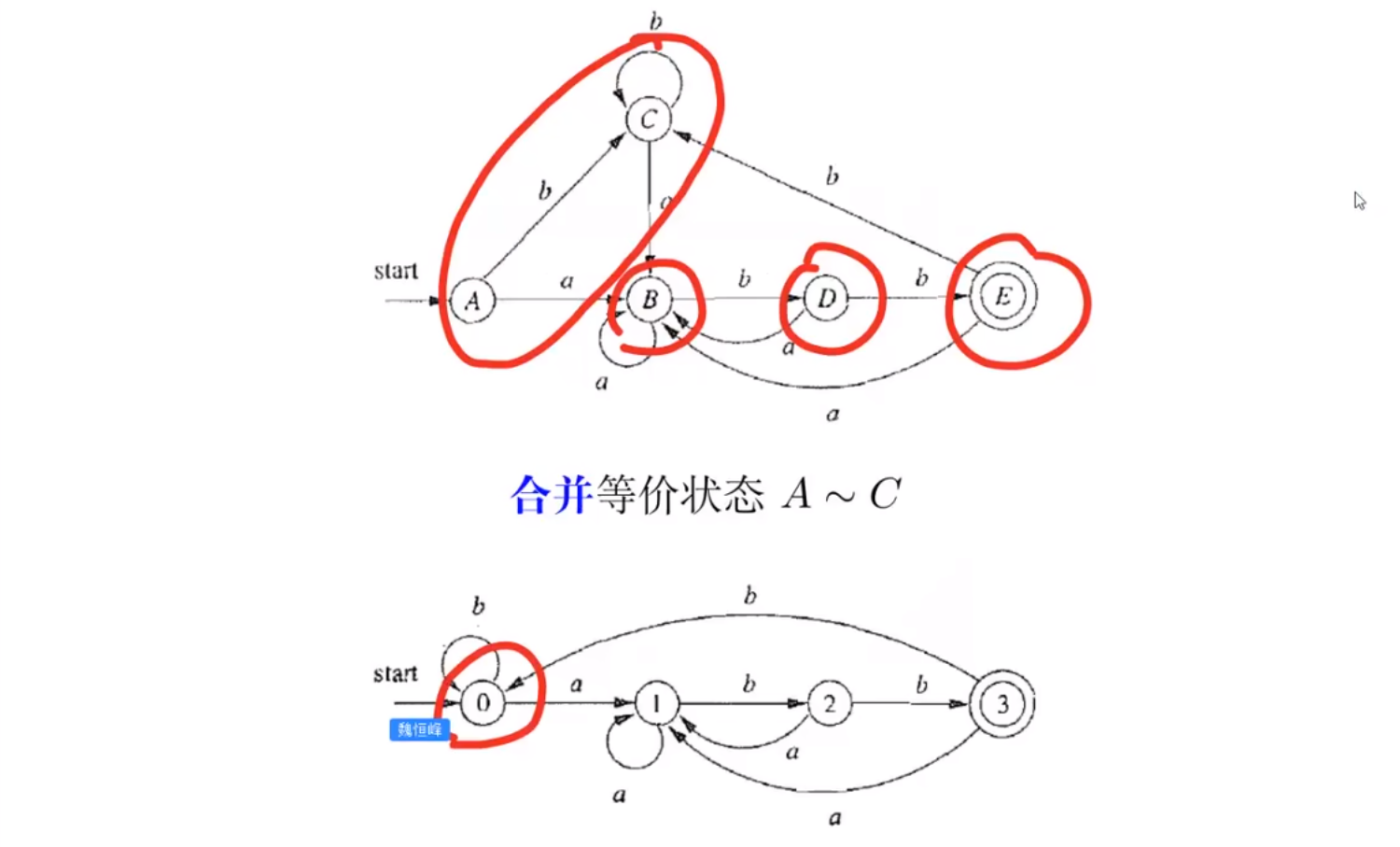
伪代码：

性质

缺点

只有DFA才能进行DFA最小化算法，有些省略的边必须补上

复杂度

todo

准确性分析

todo

最小化后唯一的吗

todo