HyperLogLog

抛硬币

在开始之前，请先玩一下下面这个游戏：

抛一个硬币，直到出现反面，记录抛硬币次数，将抛硬币次数作为分数

没错这就是课上学的伯努利过程

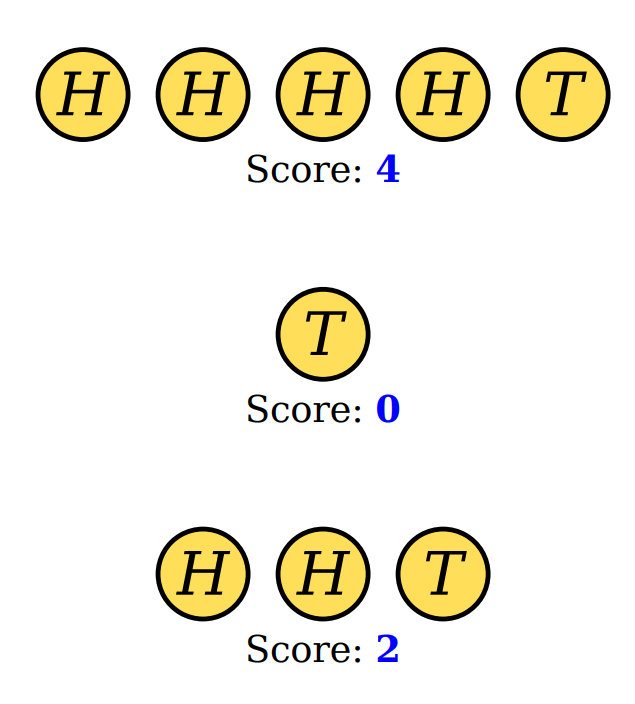
现在给你这个游戏片段，

你觉得下面哪种可能性更高呢？

1. 我运气特别好，第一次就投出来了
2. 我重复了不伯努利过程256次然后选出了最好的一次结果

一次就投出的概率：大约0.19%

256次投出的概率：大约23.3%

伯努利过程

你玩伯努利过程 $2^H$ 次，你觉得你的最好成绩是多少？

现在假设你进行伯努利实验 n 次，至少出现 k 次连续正面的概率为多少？

P &=& 1 - P[n次实验不存在连续k个正面] \\ &=& 1 - (p[一次实验抛少于k次])^n \\ &=& 1 - (1-2^k)^n

这是本文章的唯一一个公式，但是，这个函数它长啥样呢？

从硬币到基数估计

but，我们感兴趣的是构建一个基数估计器。这对我们有什么帮助呢?

想法：hash 数据流中的每个项目，并使用每个hash作为抛硬币游戏的随机来源。重复的物品会产生重复的哈希值，从而产生重复的游戏，不会对最大值有什么影响。

就像这样：

简单基数估计器

初始化一个值 $H=0$，作为伯努利实验的最好成绩。

每来一个输入，记录其伯努利实验结果，不断地更新最大值。

那么根据之前的公式，可以算得不同输入的个数差不多是：$2^H$

空间复杂度：

• 假设输入上界为 $U$，输入的hash不会超过$O(\log U)$
• hash函数要对应的最大bit位置：$O(\log \log U)$

HyperLogLog

原来的估计器的缺点：

• 答案不一定是2的幂
• 一次运气好可能会使得预测偏高

改进方案：

• 使用多个计数器
• 综合评估，去掉一个最好的之类的

HLL实现原理：

• HyperLogLog运行估计器的 $m$ 个副本，使用哈希函数将项目分配到估计器，以便每个副本得到大约 $\frac{1}{m}$ 的分数
• 计算估计的谐波平均值，以减轻异常值
• 乘以一个去偏项，以减轻来自原始估计和谐波平均值的偏倚。（该估计量在实践中得到了广泛的应用;它拥有约768字节的内存，可以估计任何真实数据流的基数，准确率约为3%。）

写在最后

本文只是斯坦福cs166的翻译：Slides09.pdf (stanford.edu)，如果您对此数据结构还是不理解，可以尝试阅读斯坦福的PPT。

算法可视化：content.research.neustar.biz/blog/hll.html