梯度下降

一种优化算法，广泛用于机器学习

# Vanilla Gradient Descent
# 梯度下降的普通版本
while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # 更新参数

细分

批量梯度下降

]

随机梯度下降

 

小批次梯度下降

 

存在问题

局部最小值和鞍点的梯度都为0，这时算法会停止，我们把这两种点统称为临界点（Critical Point）

局部最小值

对于凸问题，梯度下降算法可以很容易地找到全局最小值，但出现非凸问题时，梯度下降算法很难找到全局最小值，而模型只有找到该值才能得到最好的结果。

处理方法：

1. 局部最小值极少出现
2. 可以通过升维转化为鞍点

鞍点

我们需要梯度朝向损失函数小的地方，所以使用负特征值对应特征向量$u$作为梯度，那么$\theta ={\theta }^{\prime }+u$

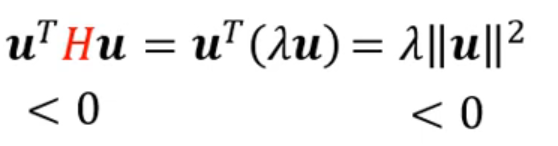
梯度消失

在梯度过小时发生。  当我们在反向传播过程中向后移动时，梯度将持续变小，导致网络中早期层的学习速度比后期层慢。 当这种情况发生时，权重参数会进行更新，直到它们接近零，这将导致算法不再学习。

梯度爆炸

在梯度太大时会发生这种情况，导致创建的模型不稳定。  在这种情况下，模型权重会变得太大，并最终表示为 NaN。 利用降维技术，可以最大程度地降低模型中的复杂性。