最小二乘法

假设采用二范数定义的平方误差来定义损失函数：

$$L(w)=\sum _{i=1}^N||w^T{x}_i-y_i|{|}_2^2$$

展开得到：

$$\begin{array}{rl}L(w)& =(w^T{x}_1-y_1,\cdots ,w^T{x}_N-y_N)\cdot (w^T{x}_1-y_1,\cdots ,w^T{x}_N-y_N{)}^T\\ & =(w^T{X}^T-Y^T)\cdot (Xw-Y)=w^T{X}^{T}Xw-Y^{T}Xw-w^T{X}^{T}Y+Y^{T}Y\\ & =w^T{X}^{T}Xw-2w^T{X}^{T}Y+Y^{T}Y\end{array}$$

现在要最小化这个值的 $\hat{w}$ ：

$$\begin{array}{rl}\hat{w}=\underset{w}{\mathrm{argmin}}L(w)& ⟶\frac{\partial }{\partial w}L(w)=0\\ & ⟶2X^{T}X\hat{w}-2X^{T}Y=0\\ & ⟶\hat{w}=(X^{T}X{)}^{-1}{X}^{T}Y=X^{+}Y\end{array}$$

这个式子中 $(X^{T}X{)}^{-1}{X}^T$ 又被称为伪逆。对于行满秩或者列满秩的 $X$，可以直接求解，但是对于非满秩的样本集合，需要使用奇异值分解（SVD）的方法，对 $X$ 求奇异值分解，得到

$$X=U\Sigma V^T$$

于是：

$$X^{+}=V{\Sigma }^{-1}{U}^T$$

在几何上，最小二乘法相当于模型（这里就是直线）和试验值的距离的平方求和，假设我们的试验样本张成一个 $p$ 维空间（满秩的情况）：$X=Span(x_1,\cdots ,x_N)$，而模型可以写成 $f(w)=X\beta$，也就是 $x_1,\cdots ,x_N$ 的某种组合，而最小二乘法就是说希望 $Y$ 和这个模型距离越小越好，于是它们的差应该与这个张成的空间垂直：

$$X^T\cdot (Y-X\beta )=0⟶\beta =(X^{T}X{)}^{-1}{X}^{T}Y$$

向量空间视角

总误差分散在N个样本点上，最小二乘法使得我们拟合出的曲线总误差最小。

第二种解释：将原来的函数改写成：

$$f(w)=w^{T}x=x^T\beta$$

这就是一个$p$维空间，使得每个样本点尽可能地在这个空间中

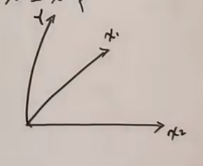
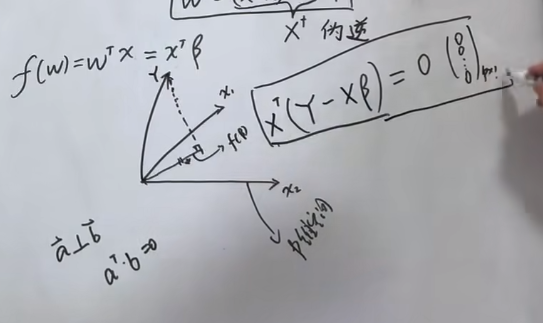
每个样本点拟合的值不一定在$p$维空间中，这时候做一个法向量$Y-x\beta$，所有的法向量都和$X$矩阵垂直。

那么现在得出结论：

$$x^T(Y-x\beta )=0$$

即：

$$\begin{array}{rl}{X}^T(Y-x\beta )& =0\\ X^{T}Y& =X^{T}x\beta \\ \beta & =(X^{T}x{)}^{-1}{X}^{T}Y\end{array}$$

概率视角

噪声成高斯分布（MLE）

最幸运的情况：所有数据都在一个直线上。

但是现实生活中的数据有噪声，这里假设噪声的概率服从一个高斯分布。

对于一维的情况，记 $y=w^{T}x+ϵ,ϵ\sim \mathcal{N}(0,{\sigma }^2)$，那么 $y\sim \mathcal{N}(w^{T}x,{\sigma }^2)$。代入极大似然估计(MLE)中：

$$\begin{array}{rl}L(w)=\log p(Y|X,w)& =\log \prod _{i=1}^{N}p(y_i|x_i,w)\\ & =\sum _{i=1}^N\log (\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}})\\ \underset{w}{\mathrm{argmax}}L(w)& =\underset{w}{\mathrm{argmin}}\sum _{i=1^N}(y_i-w^T{x}_i{)}^2\end{array}$$

这个表达式和最小二乘估计得到的结果一样。

权重先验也为高斯分布（MAP）

取先验分布 $w\sim \mathcal{N}(0,{\sigma }_0^2)$。于是： 

$$\begin{array}{rl}\hat{w}=\underset{w}{\mathrm{argmax}}p(w|Y)& =\underset{w}{\mathrm{argmax}}p(Y|w)p(w)\\ & =\underset{w}{\mathrm{argmax}}\log p(Y|w)p(w)\\ & =\underset{w}{\mathrm{argmax}}(\log p(Y|w)+\log p(w))\\ & =\underset{w}{\mathrm{argmin}}[(y-w^{T}x{)}^2+\frac{{\sigma }^2}{{\sigma }_0^2}{w}^{T}w]\end{array}$$

这里省略了 $X$，$p(Y)$和 $w$ 没有关系，同时也利用了上面高斯分布的 MLE的结果。

我们将会看到，超参数 ${\sigma }_0$的存在和下面会介绍的 Ridge 正则项可以对应，同样的如果将先验分布取为 Laplace 分布，那么就会得到和 L1 正则类似的结果。