贝叶斯决策论
马克思认为主客观在实践中统一,但是在数学上,主客观统一于贝叶斯公式。
贝叶斯决策论考虑的是基于概率,如何最小化误判损失,找到最优类别标记的算法。
将分类为的条件风险:所有误分类为的概率及其损失的和。
我们想要找到一个最优的贝叶斯分类器,与之对应的条件风险就是贝叶斯风险,反应了模型能达到的最优性能,也是模型的理论上限。
在贝叶斯模型中,最困难、最关键的是求得,为了高效、准确估计,主要分为两类模型:生成式模型、判别式模型。
- 判别式模型:直接建模,有决策树、BP神经网络、SVM
- 生成式模型:先对联合概率密度建模,有
极大似然估计
朴素贝叶斯
直接假定所有的属性是没有关系的,比如说长度、时间、摩尔数、重量。
这里由条件独立性假设重写原式:
在分类时,比较大小即可:
对于西瓜数据集:
好瓜的概率比坏瓜的概率高得多,那么会分类为好瓜。
拉普拉斯修正
如果对于离散性数据,某个属性不存在,比如说黑天鹅,那么分类为天鹅的为0,因为没见过黑天鹅,及时其他属性和天鹅一模一样

那么这时候拉普拉斯修正会给天鹅和不是天鹅类别各添加一项假数据,使得分子不是0,然后再比较大小。
半朴素贝叶斯
所有的特征之间存在某种关系,可以用算法表示出来。比如姚明和NBA。
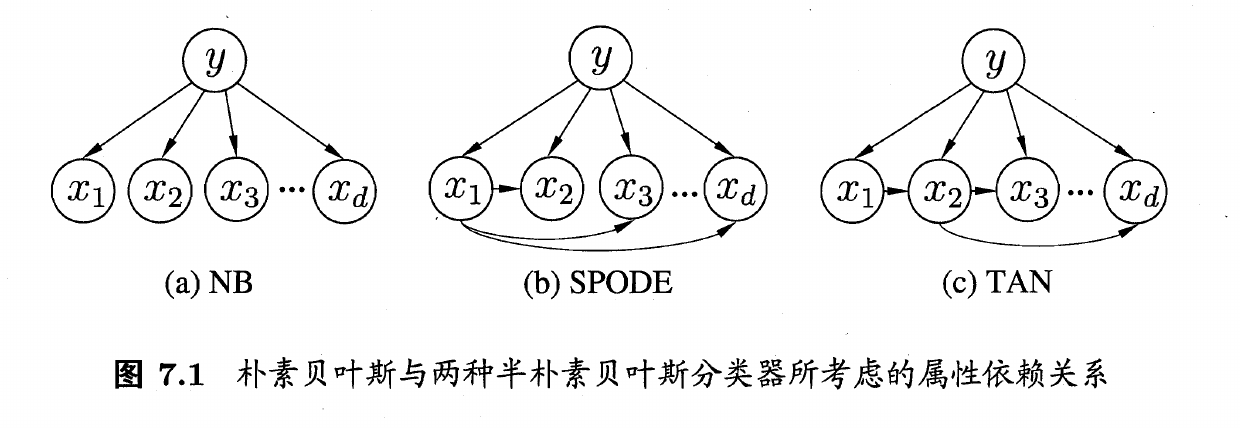
SPODE
此算法假设所有的属性都可以由一个属性导出,也就是一个超父
TAN
此算法基于最大带权生成树,通过计算属性之间的互信息,将依赖关系表达成树形结构。
贝叶斯网
一个有向无环图,节点代表实体(基因/分子),边表示因果关系。节点具有相关的概率值。
是在半朴素贝叶斯的基础上更加泛化的模型,具有更强大和灵活的建模能力,可以更准确地表示和推断变量之间的复杂关系。
贝叶斯网络的建模过程:
- 确定变量:确定要建模的变量,并为每个变量选择适当的离散或连续值域。
- 构建结构:确定变量之间的依赖关系,并使用有向边连接节点。这可以通过领域知识、统计分析或专家判断来完成。
- 参数化:为每个节点的条件概率表(CPT)分配参数。这些参数表示给定其父节点的情况下,每个节点取各个值的概率。
- 推理:利用贝叶斯网络进行推理和预测。给定一些观测值或证据,可以计算后验概率分布,并回答关于其他变量的查询问题。
EM算法(Expectation-Maximization Algorithm)
EM算法(Expectation-Maximization Algorithm)是一种迭代优化算法,用于在存在隐变量的概率模型中估计参数的最大似然估计或最大后验概率估计。
下面是EM算法的基本步骤:
-
初始化:选择初始参数的估计值。
-
E步骤(Expectation Step):在E步骤中,计算隐变量的后验概率(给定观测数据和当前参数估计),并将其作为隐变量的期望值。
-
M步骤(Maximization Step):在M步骤中,使用E步骤中计算得到的隐变量的期望值,通过最大化完全数据的对数似然函数或对数后验概率函数来更新参数的估计值。
-
迭代:重复执行E步骤和M步骤,直到参数估计收敛或达到预定的停止条件。
EM算法的核心思想是通过迭代的方式,通过观测数据和隐变量的期望值来更新参数的估计值。在每一次迭代中,E步骤用于计算隐变量的期望值,M步骤用于最大化似然函数或后验概率函数来更新参数的估计值。通过反复迭代,EM算法逐渐优化参数估计,直到达到收敛的参数估计。
EM算法只能找到一个局部最优解。因此,在使用EM算法时,初始参数的选择对结果可能有较大的影响。