维度灾难

简介

维度灾难的概念最早由Richard E. Bellman在研究动态规划算法时提出，是指当维度升高时，会遇到低维场景下察觉不到的困难。对机器学习来说，维度升高带来的一个明显“灾难”是数据稀疏。

一个病人去看病，给医生描述自己的情况。他说：“我身高173cm，体重73kg，年龄23岁。”然后医生又给他量了血压、心率、骨密度、血氧含量等等一系列指标。在这个过程中，描述这个病人的指标（feature）越来越多，他和其他所有人比起来显得越来越独特。打个更夸张的比方，当你用人全身上下每个毛囊里的发丝数量来描述每个人，用于描述每个人的向量的dimension超级大，每个人都是那么的独一无二，任何两人之间的差别都大到你无法理解的程度。你现在拉来一对黄种人同卵双胞胎，再拉来一个白种人，数他们每个毛囊里发丝的数量。虽然双胞胎是那么相似，但从毛囊发丝数量的角度来看，两者还是差别非常大。在你看来，这俩双胞胎和那个白人都是一样的与众不同，你根本无法感知到双胞胎之间的相似性。这就是Curse of Dimensionality，当你从非常多的角度去描述事物，每个事物之间的差距都非常大，大到你觉得都一样大，大到你感知不出不同物体之间的细微的相似之处。

每个物体都是一样地与众不同，又谈何归类和分析呢？

作者：PFAL

例子

假设我们有一个“猫狗”数据集，输入是图片，输出是类别。

这是一个最简单的线性分类器：

# 仅使用RGB三原色的分类器
if 0.5*red + 0.3*green + 0.2*blue > 0.6 : return cat; 
else return dog;

这当然无法将猫狗完美地分类，我们可能还需要其它特征，譬如毛发、平均边缘、梯度等，早期的AI工程师就是这样通过手工构造特征来拟合数据的。

但是，是不是特征越多，效果越好呢？

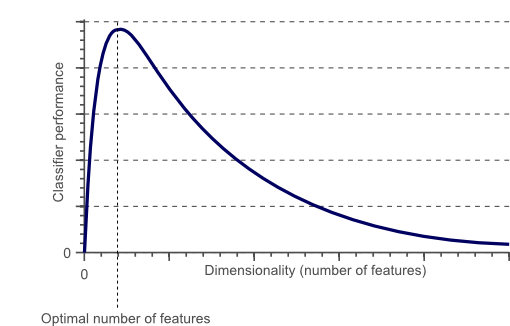
并不是！如上图所示，随着维度的增加，分类器的性能的确会提高，但是在达到某个最佳特征数量的位置后，在不增加训练样本数量的情况下进一步增加维度反而会导致分类器性能下降。这就是维度灾难(The Curse of Dimensionality).

维度灾难与过拟合

在前面介绍的猫和狗的例子中，让我们假设生活在我们的星球上的猫和狗的数量是无限的。但是，由于我们的时间和处理能力有限，我们只能获得 10 张猫和狗的照片。分类的最终目标是仅根据这 10 个训练实例训练一个分类器，该分类器能够正确分类我们没有任何信息的无限数量的狗和猫实例。

让我们仅使用单个特征分类，比如红色：

你会发现，猫狗混在一起，根本无法分类。

那再试试两个特征，比如红色和绿色：

看起来更清晰了，不过还是无法分类，因为我们无法找到一条直线将其分割。

最后试试三个特征：RGB

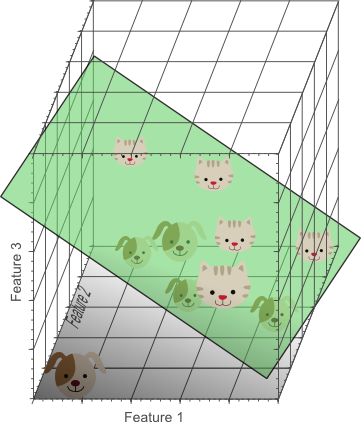
Nice！我们产生了一个三维特征空间，将所有的猫狗图片完美分类了。这意味这使用三个特征组合，在我们的10张图片的训练数据上去获取了完美的分类结果。

让我们再次添加特征：

你会发现我们的模型在投影到二维后，将猫的特征分成了三类，每个单独圈了起来，这发生了**过拟合。高维空间训练形成的线性分类器，相当于在低维空间的一个复杂的非线性分类器，这种分类器过分强调了训练集的准确率甚至于对一些错误/异常**的数据也进行了学习，而正确的数据却无法覆盖整个特征空间。

如果我们有更多甚至无限的数据，那么在更高的维度下，我们的分类器也许可以正确分类。

但是，为什么在高维更倾向于过拟合呢？这里引入数据稀疏性。

数据稀疏性

在10个猫狗图片的数据集上，如果我们继续添加特征，特征空间的维数就会增长，你会认为找到可分离的超平面变得更加容易，这里的容易实际上指的是特征空间变稀疏了。

解释1

重新解释一下之前的内容：

假设我们只使用一个特征来训练分类器，1D特征值的范围限定在0到1之间，且每只猫和狗对应的特征值是唯一的。

如果我们希望训练样本的特征值占特征值范围的20%，那么训练样本的数量就要达到总体样本数的20%。

现在，如果增加第二个特征，也就是从直线变为平面2D特征空间，这种情况下，如果要覆盖特征值范围的20%，那么训练样本数量就要达到总体样本数的45%(0.45^2=0.2)。

而在3D空间中，如果要覆盖特征值范围的20%，就需要训练样本数量达到总体样本数的58%（0.58^3=0.2）。

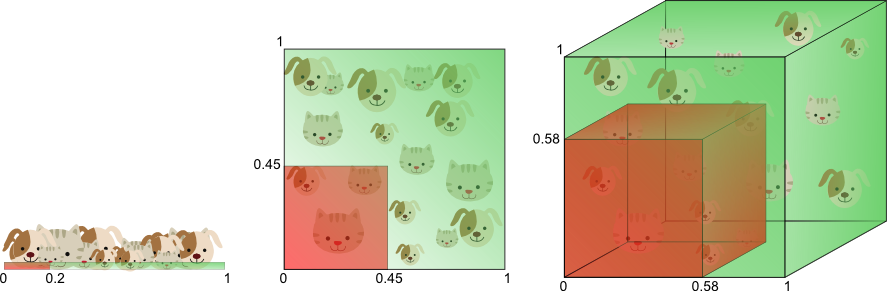
换一种解释，我们假设在一维空间中，每隔0.1就要有一个样本，这一共需要10个样本就能满足。但是对于二维的情况，仍然限定每隔0.1就要有一个样本，那么这时候需要100个样本。上升到n维，就是$10^n$个样本。维度越高，其训练需要的样本数也就越大，因为很多机器学习算法都是基于距离衡量的。

解释2

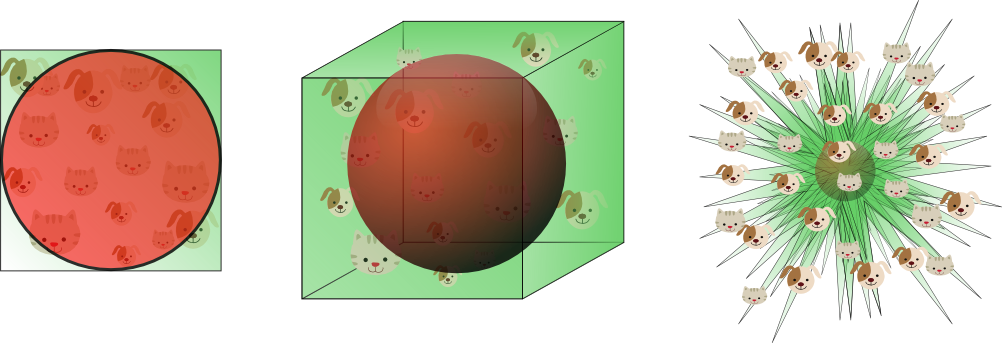
假设这个边长为1正方形表示二维的特征空间，特征空间的平均值是这个正方形的中心，离这个圆点中心距离为0.5的样本分布在位圆中。这个圆的集合含义就是咱们的搜索空间。

不再圆内的样本距离角落和相比圆心更近，如果样本都落在了圆内，分类将会很简单；如果样本落到了圆外（边角部分)，就会很难分类。

这个二维的圆有，占了$\pi \ast 0.5^2=0.79$的空间，对于三位的圆，一共占了$\pi \ast 0.5^3=0.53$的空间。对于$n$维度的圆一共占了$\frac{{\pi }^{d/2}}{\Gamma (\frac{d}{2}+1)}\ast 0.5^d$的空间，搜索空间越来越小。

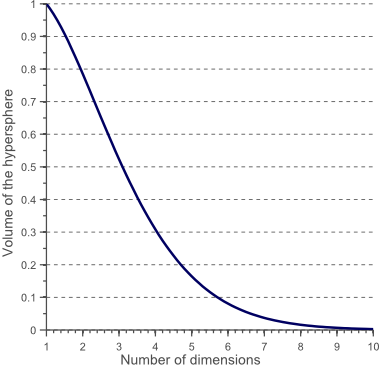
那么这就导致维度越高，数据就越靠近边界，新的实例很可能远离任何一个训练实例，导致跟低维度比起来，预测更加的不可靠，更容易过拟合。

当特征空间的维度变得无限大时，从样本点到质心的最大、最小欧氏距离的差值与其最小欧式距离的比值趋于零：

$$\underset{d\to \infty }{\lim }\frac{dis{t}_{max}-dis{t}_{min}}{dis{t}_{min}}\to 0$$

因此，距离测量在高维空间中逐渐变得无效。因为分类器是基于这些距离测量的（例如Euclidean距离、Mahalanobis距离、Manhattan距离），所以低维空间特征更少，分类更加容易。同样地，在高维空间的高斯分布会变平坦且尾巴更长。

解释3

在解释2基础上，我们求一个环形带的体积：

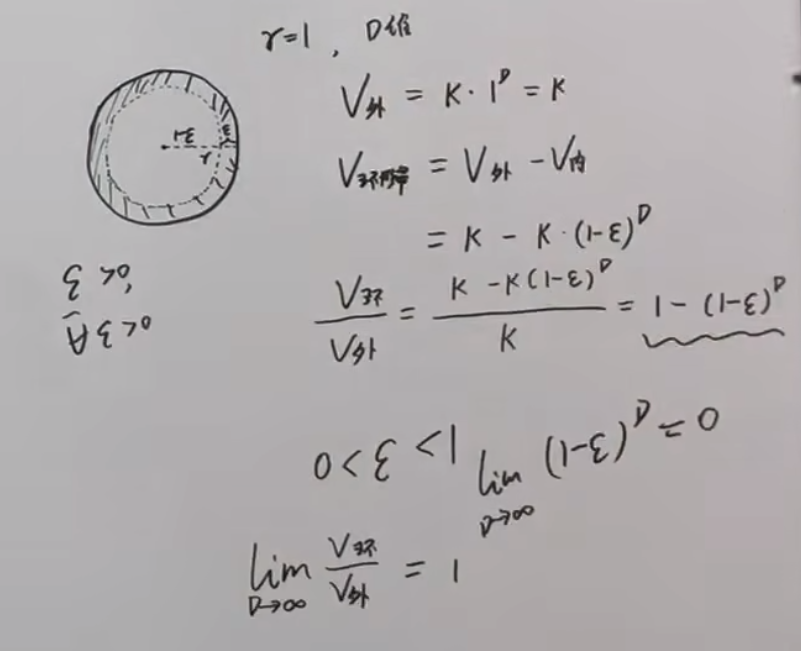
在维度无限高的情况下，环形带的体积和整个球的面积的极限为1。

因此，如果在高维下拟合数据集，你会发现全部集中于球壳上面，即恰好将整个数据集包裹起来。

解决方法

  在处理维度灾难的时候，我们可以通过增加数据集、正则化、降维等方法来解决。

  虽然增大数据集可以使训练实例达到足够的密度，可以解决维度灾难的问题。但是要达到给定密度，所需要的训练集数量随着维度的增加呈指数式的上升。比如100个特征，要让所有训练实例(假设在所有维度上平均分布)之间的距离小于0.1，这时需要的训练实例数量就比可观察的宇宙中的原子数量还要多…所以在解决维度灾难时，我们常常会采用降维。

  对于降低维度，我们主要有三种方法：

• 直接降维 : 特征选择（人工或者自动。如Lasso方法）
• 线性降维 : PCA、MDS
• 非线性降维：流行学方法，包括Isomap 以及 LLE(局部线性嵌入)方法

不同算法维度权衡

  当模型比较复杂时，不要选择太高的维度；当模型比较简单时，可以选择较高的维度。其实就是要去考虑：是否要去增加维度，提供非线性的问题。

• 非线性决策边界的分类器（例如神经网络、KNN分类器、决策树等）分类效果好但是泛化能力差且容易发生过拟合。因此，维度不能太高。
• 使用泛化能力好的分类器（例如贝叶斯分类器、线性分类器），可以使用更多的特征，因为分类器模型并不复杂。 因此，过拟合只在高维空间中预测相对少的参数和低维空间中预测多参数这两种情况下发生。

References

1. 如何通俗的理解维度灾难问题？ - 知乎
2. The Curse of Dimensionality in Classification
3. 2110.09485.pdf