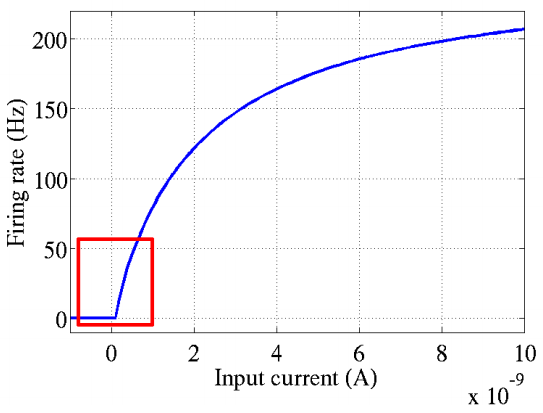
经元的激活函数,ReLU起源于神经科学的研究:2001年,Dayan、Abott从生物学角度模拟出了脑神经元接受信号更精确的激活模型,如下图:
ReLU的定义
ReLU是Rectified Linear Unit的缩写,中文名叫修正线性单元。它是一种常用的神经网络激活函数,其数学定义为:
f(x) = max(0, x)
其函数图像如下:

Softplus可以看作ReLU的平滑版本
优点
与Sigmoid、Tanh等传统激活函数相比,ReLU有以下优点:
-
单侧抑制:左侧被抑制
-
计算简单高效: ReLU只需要和0比较大小,不涉及指数等复杂计算。这使得神经网络的训练更加高效。
-
减轻梯度消失问题: Sigmoid等函数在两端都容易出现梯度接近0的现象,导致深层网络难以训练。而ReLU在x>0时梯度恒为1,一定程度上缓解了梯度消失。
-
提供了稀疏性: ReLU会将一部分神经元的输出置为0,引入了稀疏性,使得网络可以学习到更加紧凑的特征表示。
-
更符合生物学特性: 相比Sigmoid等函数,ReLU更接近生物神经元的激活特性。
缺点
ReLU虽然有诸多优点,但也存在一些问题:
-
死亡ReLU问题 - 当某个神经元的输入持续为负,其输出就会一直为0,不再对网络学习做出贡献,这种现象叫”死亡ReLU”。
-
输出无上界 - 与Sigmoid等函数不同,ReLU输出没有上限,这可能导致部分神经元的值变得很大,影响网络稳定性。
变体
为了解决这些问题,研究者提出了一些ReLU的变体,如Leaky ReLU、PReLU、ELU等。它们在保留ReLU优点的同时,对缺点进行了一定改进。
总之,ReLU激活函数易于实现、计算高效,能有效缓解梯度消失,已成为目前最常用的激活函数之一。理解ReLU的特性,有助于更好地设计和优化神经网络模型。